Bearing And Distance With Solved Examples
Bearing and distance is one of the applied knowledge of trigonometry. So in majority of the textbook for SS1, SS2, SS3, and those in high schools. It falls under trig (1) and trig (2).
Bearing can be defined as the angular relationships between two or more places. The four main directions are North (N), South (S), West (W), and East (E). The sub-directions are North-West (NW), North-East (NE), South-West (SW), and South-East (SE).
The angular relationship between two or more places can be expressed as compass or three digit notation.
How to Solve Questions on Bearing And Distance
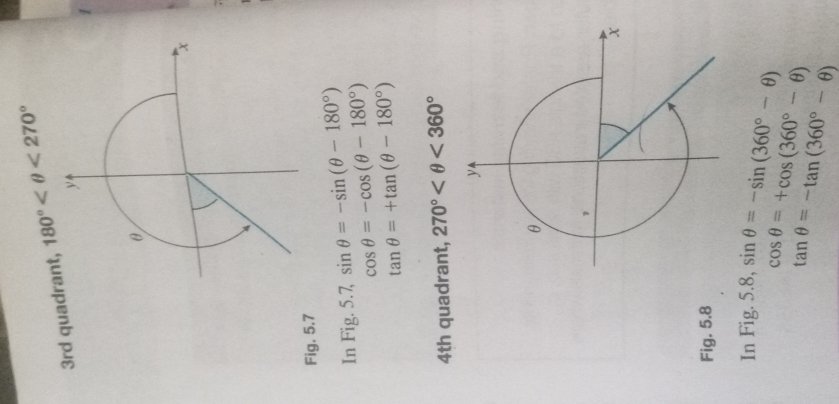
Firstly, you must know that the cartesian axes Ox and Oy divide the plane into the 1st, 2nd, 3rd, and 4th quadrants.
For trigonometric purposes, an angle is defined as a measure of the rotation of a line about the origin, starting from the direction Ox. The angle may be positive or negative depending on whether the rotation is anticlockwise or clockwise.
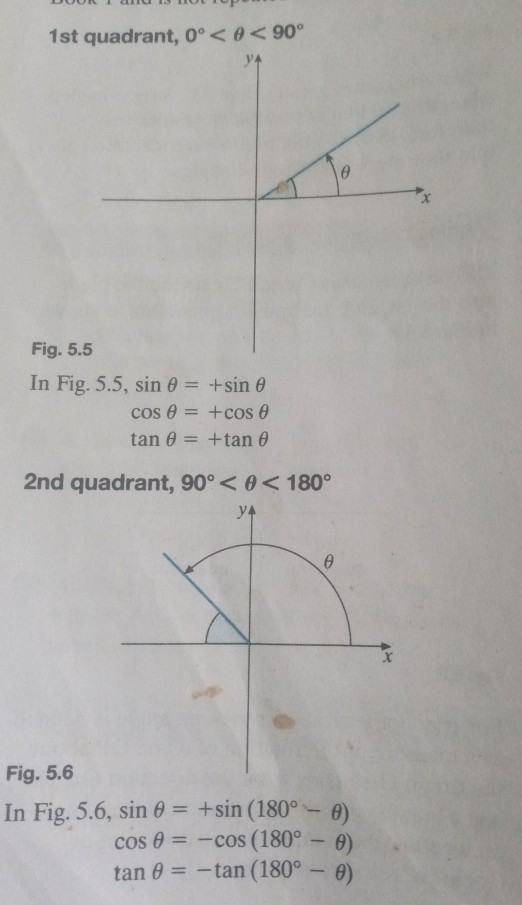
To solve any question on bearing and distances, you must use either sine rule or cosine rule.
Sine rule
In any triangle ABC, the angles are usually denoted by the capital letters A, B,C and the sides opposite these angles by a, b, c respectively.
a/sinA = b/sinB = c/sin C
This formula is used for solving triangles which are not right-angled and in which either two angles and any side are given or two sides and the angle opposite one of them are given.
Example 1
A point X is 34m due east of a point Y. The bearings of a flagpole from X and Y are N18oW and N40oE respectively. Calculate the distance of the flagpole from Y
Solution
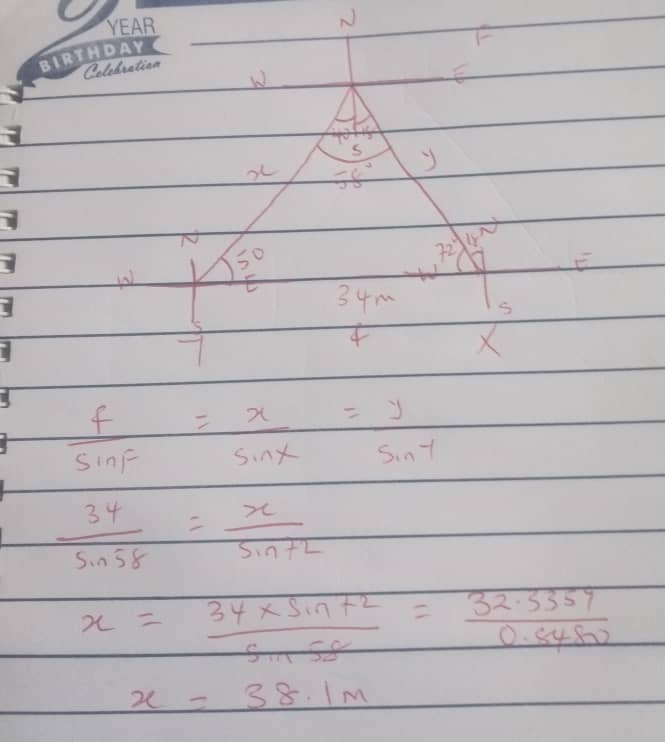
Cosine rule
c^2 = a^2 + b^2 -2ab cosC
b^2 = a^2 + c^2 -2ac cosB
a^2 = b^2 + c^2 -2bc cos A
this formula is for solving triangles which are not right-angled in which two sides and the included angle are given.
Example 2
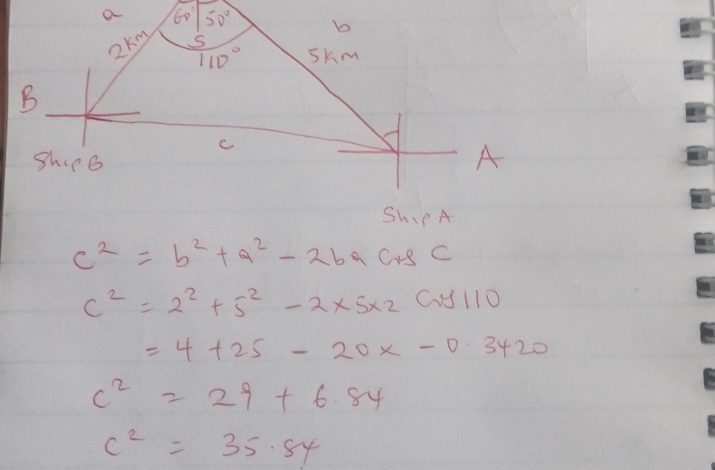
From a point on the edge of the sea, one ship is 5km away on a bearing S50oE and another is 2km away on a bearing S60oW. How far apart are the ships?
Solution
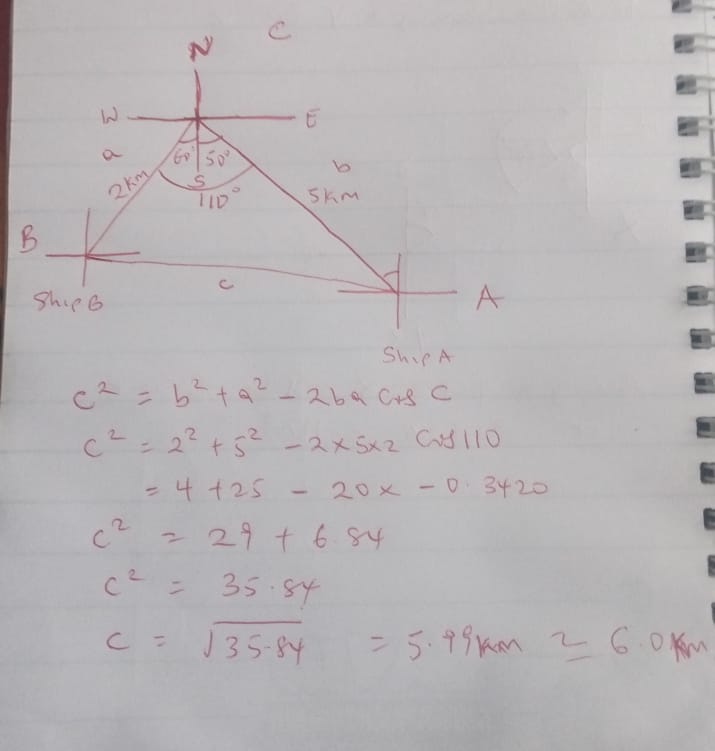
Read: Make a the subject of the formula v = u + at
Solved Examples on Bearing and Distance
Compass Bearing
This bearing can be represent in the sub-direction i.e. North-West (NW), North-East (NE), South-West (SW), and South-East (SE). For example, N30oE, S50oW, S20oE
Example 3
Express the true bearing 210o as compass bearing
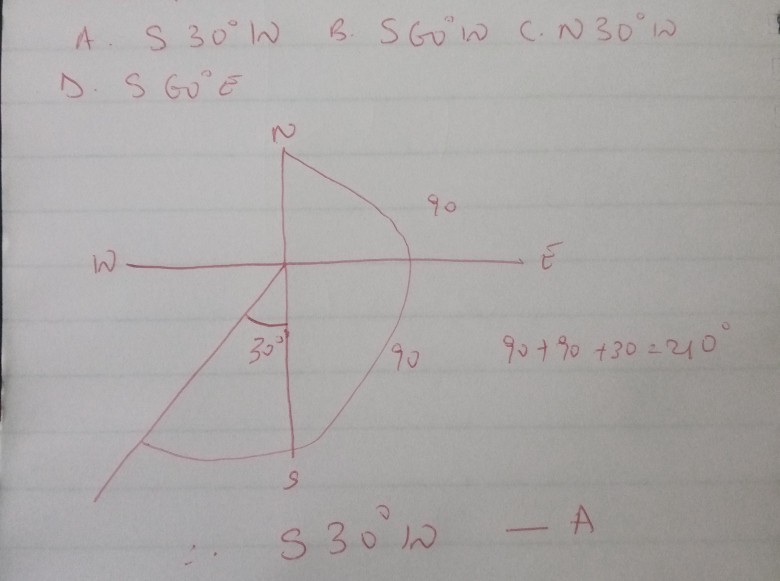
Three digit notation
This is measured clockwise from the North. For example, 020o, 215o, 309o, etc.
Example 4
What is the equivalent of S70oE in three digit notation?
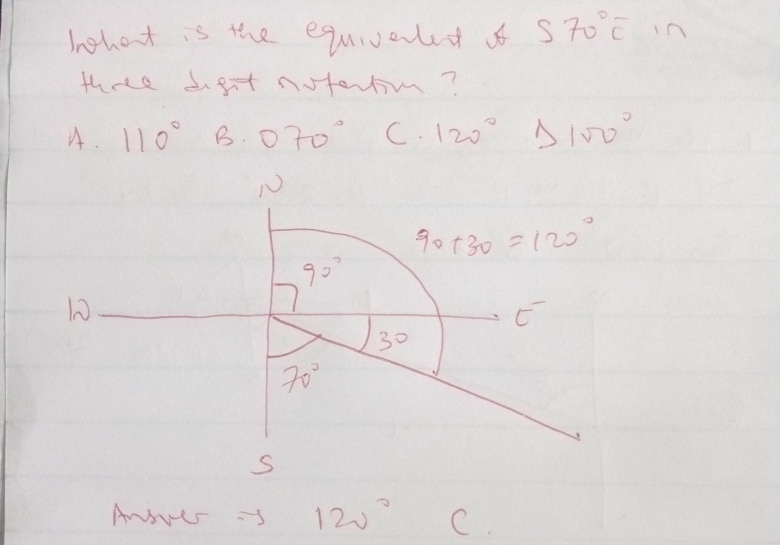
Example 5
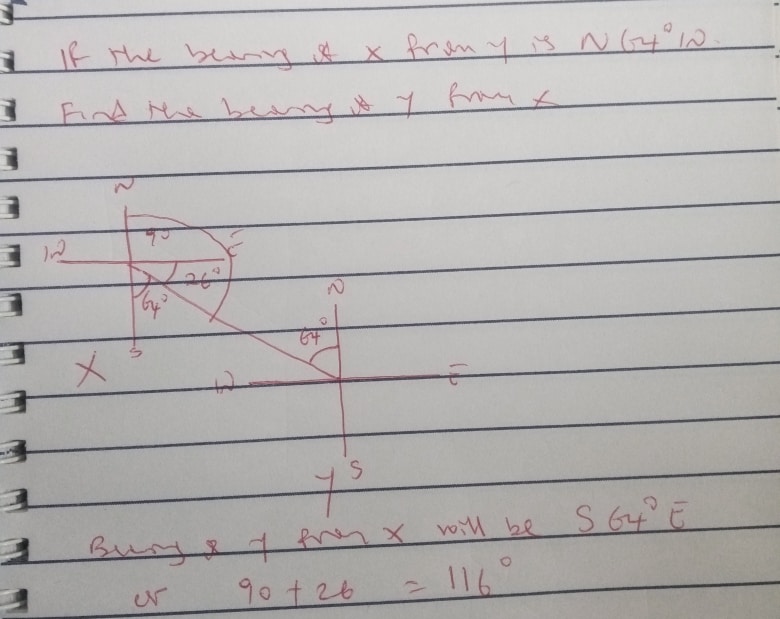
If the bearing of X from Y is N640W. Find the bearing of Y from X.
Example 6
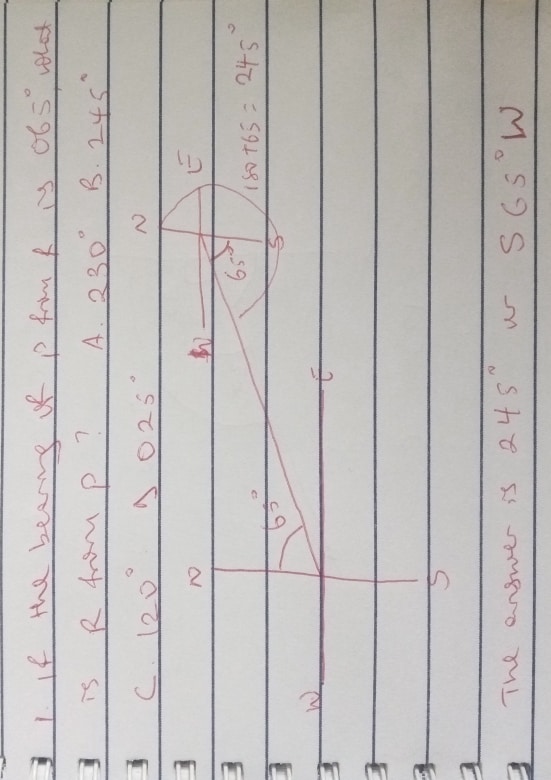
If the bearing of P from R is 0650, what is R from P? A. 2300 B. 2450 C. 1200 D 0250