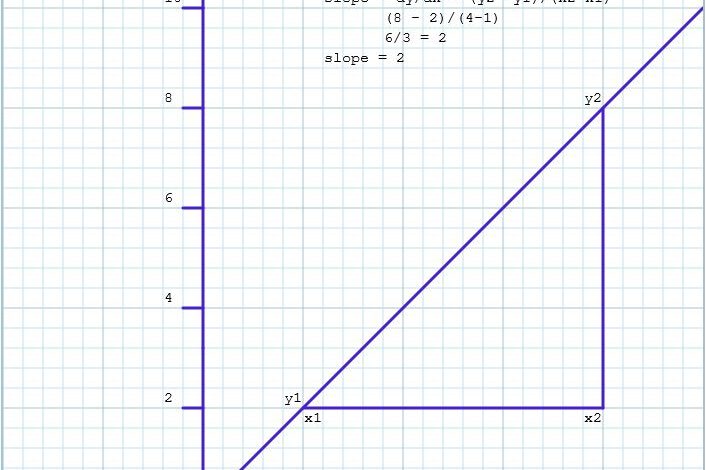
When plotting a graph in mathematics or physics, you may be asked to find the slope of the graph, and in the process, you might get an undefined slope or zero slope. So, because of these instances, I will discuss how you can differentiate between the two slopes.
Undefined Slope
This idea is gotten from an undefined fraction. An undefined fraction is a fraction where the denominator is equal to zero.
And to find the slope of a graph, we already know that, dy/dx = 0 or y2 -y1/x2-x1 = 0. So, to get this slope, the change in x i.e. dx (x2-x1) = 0. And the implication is that x2 = x1 to have an undefined slope.
Therefore, for a slope to be undefined, the line will be vertical (the second and first coordinate of x has the same value).
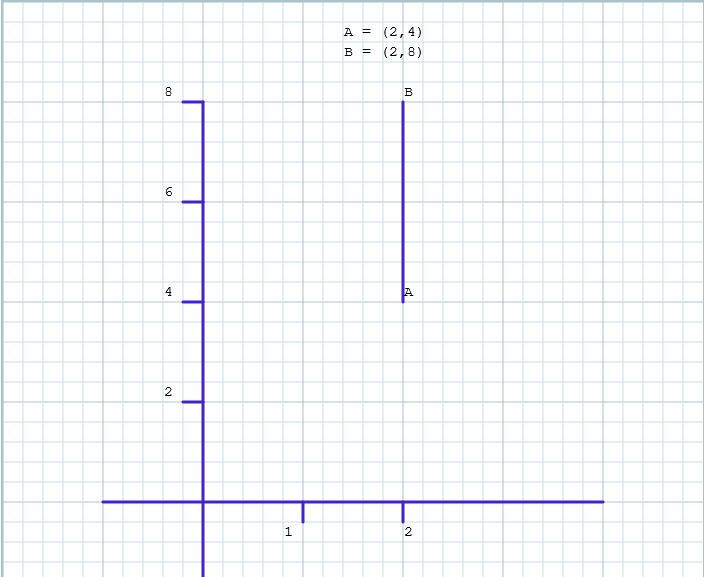
Zero Slope
To have a zero slope, the change in y (dy) will be equal to zero i.e. y2 – y1 = 0. What this means is that, the second and first coordinate of x has the same value. And for this to be possible, y2 = y1. Since the change in y is at the numerator when finding the gradient of a line, then the numerator will be zero.
Therefore, for a slope to be zero, the line will be horizontal.
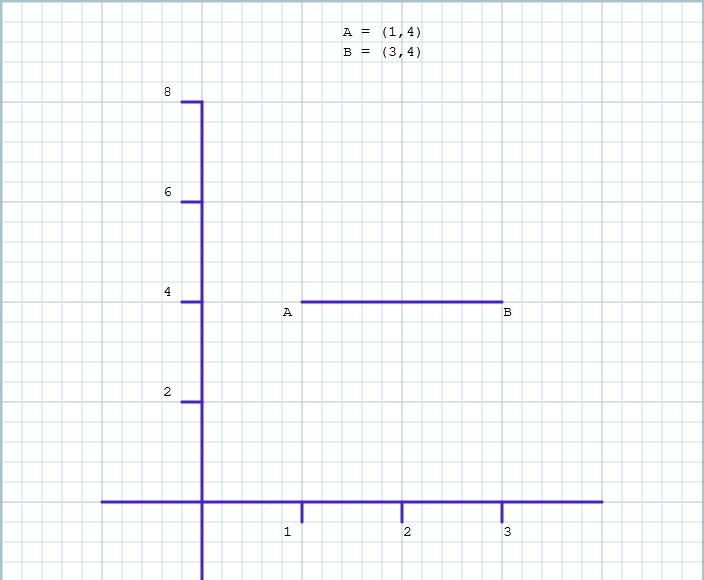
Differences Between Undefined and Zero Slope
| Undefined slope | Zero slope |
| It is determined the x-coordinate. | It is determined by the Y-coordinate. |
| The two values in the x-coordinate is the same. | The two values in the y-coordinate is the same |
| The line is vertical | The line is horizontal |
| The denominator of the undefined slope is zero. | The numerator of the zero slope is zero. |
