How To Use Logarithm Table And Download Four Figure Table Pdf
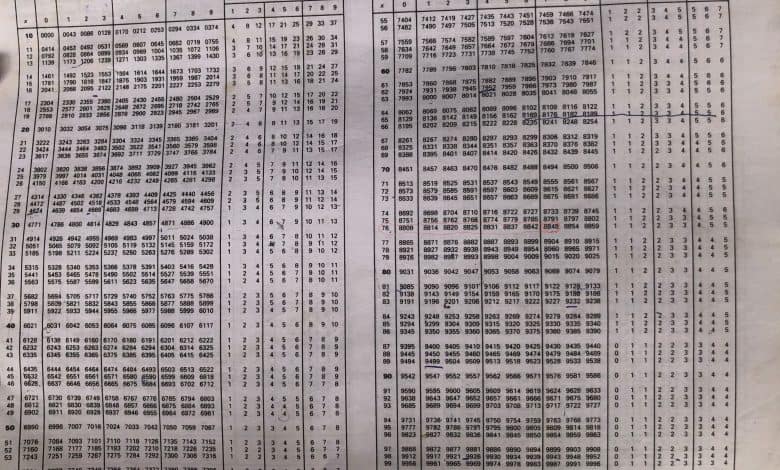
A logarithm table is used to find the log and antilog of numbers. This is very useful when finding the multiplication and division of numbers. Before I put you through how to use it, you need to know how to convert numbers to standard form.
Kindly note that the link to download four figure table, which has both the logarithm and antilogarithm table has been provided below.
How to Find Logarithm Of a Number From Table
The logarithm of a number is in two parts, the characteristics and the mantissa. For example, 2.5735 has (2) as the characteristics(integer) and (.5735) as the mantissa.
If a number is in standard form, it is easy to see what the characteristics of its logarithm is.
(1) For example, log 734 has the characteristics of 2 i.e.
734 = 7.34 x 102 in standard form
It is also worthy noting that when using logarithms to perform calculations, we assume that the base is 10.
Let me now show you how to make use of the logarithm table to find the log of numbers below
Log 76.7

Firstly express 76.7 in standard form and that will be 7.67 x 101
So, log 76.7 = 1.
Now the other value after the decimal point will be:
- Go to your logarithm table and check where 76 is
- After you have found 76, you will see numbers (0-9) at the top
- You will then look for the value of 76 under 7 and that will be 8848
So log 76.7 = 1.8848
To find the logarithms of numbers less than 1 we use negative powers of 10. This kind of number do have negative characteristics and a positive mantissa.
For example
(2) find log 0.005812 using table
The first thing is to express the number in standard form
0.005812 = 5.812 x 10-3
So log 0.005812 = -3 or bar 3
Then look for where 58 is in the table, and check through the value under 1
So 58 under 1 is 7642, then difference 2 is (1)
So 58 under 1 difference 2 is (7642 + 1 = 7643)
Therefore, log 0.005812 = -3 + 0.7643 = bar(3).7643
How to Find Anitlog Using Table
For example, use antilogarithm tables to find the number whose logarithm is 4.8625
Solution
Let the number be n
Log n = 4.8625
N = antilog of 4.8625
= 104.8625
= 104 + 100.8625
= 10000 x (this will be .86 under 2 difference 5) (7278 + 8 = 7286, this is then 7.278)
= 10000 x 7.278
= 72780
Therefore, the antilog of 4.8625 is 72780
How to Use Log Table for Multiplication and Division
To multiply and divide numbers, first express them as logarithms and then apply the addition and subtraction laws of indices to the logarithm. Steps to follow
Kindly note that multiplication will be addition while division will lead to subtraction
- Use the logarithm tables to change the numbers to logarithms
- Finally, use the anti-logarithm tables to change the logarithms back to numbers
Example, calculate (76.7 x 308.2) / 8.04
Solution
| Number | log |
| 76.7 308.2 | 1.8848 +2.4889 |
| 4.3737 | |
| 8.04 | -0.9053 |
| 3.4684 | |
Next is to find antilog of 3.4684
Log n = 3.4684
N = antilog of 3.4684
= 103.4684
= 103 + 100.4684
= 1000 x 2.941
= 2941
So, (76.7 x 308.2) / 8.04 = 2941
Download Free Four figure Table pdf
The values are given to 4 places of decimals, hence the term, four-figure tables. Each table consists of two pages, lying facing on another. On the leftmost column you can see values of x being listed, in differences of .00 to 99 and in another case 10 to 99
On the row, x travels from 0 to 9, and the ‘differences’ side runs from 1 to 9 as well and this is the mean difference, which must be added to obtain the final value.
To download four figure table, click here
