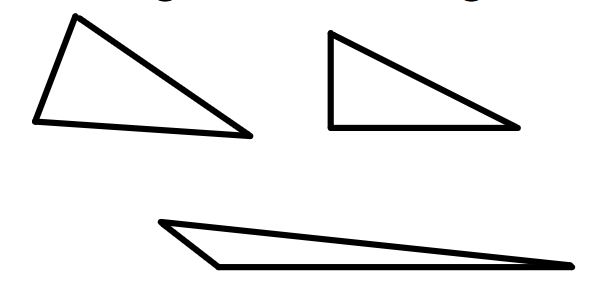
In this article, I will discuss the definition, properties, area, perimeter, and some examples of scalene triangle.
A triangle is a closed figure in a plane consisting of three segments called sides. Any two sides intersect in exactly one point called a vertex.
A triangle can be classified according to its sides, angles, or a combination of both. Classification of triangles according to its sides are
- Equilateral
- Isosceles
- Scalene
A triangle with all three sides equal in length is known as an equilateral triangle. A triangle with two sides equal in length and the third side different is known as an isosceles triangle. If the measurement of all the three sides of a triangle is unequal, then the triangle is known as the scalene triangle.
Definition of Scalene Triangle
A scalene triangle is a type of triangle with all three sides are not equal in length, and also all the three angles of a scalene triangle is different. However, the sum of all the interior angles of a scalene triangle is always equal to 180 degrees.
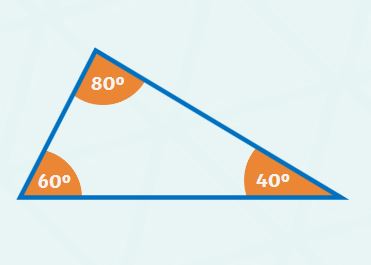
Properties of Scalene Triangle
Some of the properties of the scalene triangle are as follows:
- A scalene triangle can be an obtuse-angled, acute-angled or right-angled triangle.
- It has no equal sides.
- It has no equal angles.
- It has no line of symmetry.
- It has no point symmetry.
- The angles inside this triangle can be an acute, obtuse or right angle.
- All of its interior angles are different – but they still add up to 180º.
Area of Scalene Triangles (Formula)
Finding the area of a scalene triangle might be a bit taxing because the triangle has no equal sides nor equal angles.
The formula to use to find the area depends on the information given about the triangle
Area of scalene triangle formula when any side considered as base ‘b’ and height ‘h’ (a perpendicular drawn from the base) is given as:
Area = ½ × base(b) × height(h)
If all the three sides of a triangle are given, then the area of a triangle can be calculated using Heron’s formula.
Area of the triangle = [sqrt{S(S – a)(S – b)(S – c)}] square units
Where, s is the semi perimeter of a triangle, which can be found using the formula
s = (a+b+c)/2
where, a, b, and c denotes the sides of the triangle
Perimeter of a Scalene Triangle
The perimeter of a triangle is equal to the sum of the length of sides of a triangle and it is given as:
Perimeter = a + b + c units
Example: Find the perimeter and the area of the scalene triangle below.
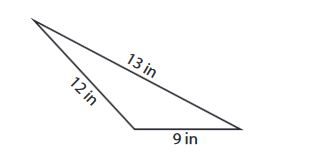
Solution: The perimeter is a + b + c = 13 + 12 + 9 = 34 in
Area = [sqrt{S(S – a)(S – b)(S – c)}]
S = (13+12+9)/2 = 34/2 = 17
Area = sqrt{17(17-13)(17-12)(17-9)} = sqrt{17(4)(5)(8)} = sqrt (2720) = 52.15 in2
Read: Area of a trapezium
