Supplementary Angles Definition And Examples
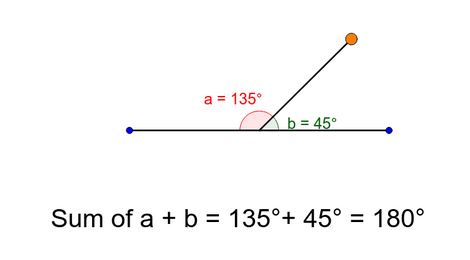
For two angles to be supplementary, their sum must be 180 degree. Examples of supplementary angles are 140o and 40o, 150o and 30o, 100o and 80o, 160o and 20o, etc. In most cases, supplementary angles are gotten on a straight because the sum of angles on a straight line is 180 degree. The moment the angle on a straight line is bisected, the two angles formed will be supplementary.
The supplementary angle theorem states that if two angles are supplementary to the same angle, then the two angles are said to be congruent.
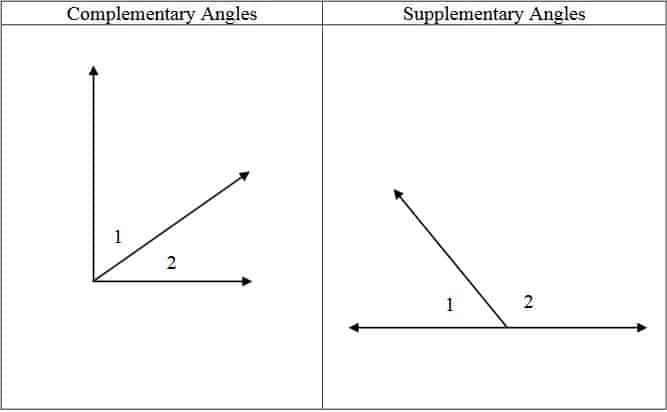
There is another concept called complementary angles, the two angles add up to 90 degrees. Below I will give the differences between supplementary and complementary angles in tabular form.
Read: Examples of Corresponding angles
Differences Between Supplementary and Complementary Angles
| Supplementary | Complementary |
| The two angles sum up to 180o | The two angles sum up to 90o |
| They form a straight line when combined together. | They form a right-angled triangle when combined together. |
| The supplement of an angle X is (180 – X)° | The complement of an angle X is (90 – X)° |
FAQ On Supplementary Angles
Do supplementary angles form a linear pair
Yes, two supplementary angles always form a linear pair because they sum up to 180 degrees. And the sum of angles on a straight line is 180o
Are two right angles always supplementary
Yes, because the sum of two right angles is 180o.
Can two obtuse angles be supplementary to each other
No. An obtuse angle is an angle greater than 90°. Let us take the least obtuse angle which is 91, it supplement will be 89, and 89 isn’t an obtuse angle. So, two obtuse angles can’t be supplementary to each other.
Are supplementary angles congruent
The condition for this to be so is that If two angles are supplementary to the same angle, then they are congruent to each other. For example, if angle A is supplementary to C and angle B is supplementary to C, then angle A and B are congruent.
Proof
<A + <C = 180
<A = 180 – <C
Also,
<B + <C = 180
<B = 180 – <C
Therefore, <A = <B (congruent)
Congruent angles are the angles that have equal measure
Are the opposite angles of a kite supplementary
In a kite the opposite angles are equal, so for it to be supplementary, the opposites angles must be 90o. This means when the opposite angles of a kite is 90o, they are supplementary.
Supplementary Angle Examples
Question 1: An angle is five times its supplement. Find both angles.
Solution
Let the angle be x, and its supplement will be (180-x)
According to the question, x = 5 *(180-x)
x = 900 – 5x
6x = 900
x = 900/6 = 150
Then it supplement will be, 180 – 150 = 30
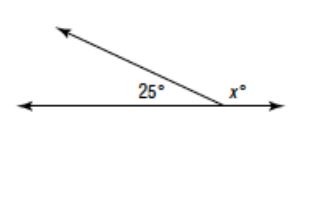
Question 2: Find the missing measurement in the pair of angles

Solution: x + 25 = 180 (supplementary angle)
x = 180 – 25 = 155 degree
