Understanding Centre of gravity of an Object

How to determine the centre of gravity of an object and concept of centre of gravity is what students of physics ought to understand especially when answering questions on moment of forces or rotational motion in classical mechanics.
Every particle or object has weight because of the force of gravity on them, said differently; every object is attracted towards the centre of the earth by the gravitational force. The point where all the weight of the object may appear to act is referred to as centre of gravity.
Stability of an object (stable, unstable, and neutral) depends on the CG of that object. There are factors that affect the C.G. of an object, they are:
- The distribution of the masses
- The gravitational free strength which is the same as acceleration of free fall g
How to find the centre of gravity
It is easier to find the centre of gravity of a regular object (uniform object) than irregular object. The C.G of a uniform object is at its mid-point.
- The C.G for a person standing upright is in the middle of the body behind the navel
- The C.G of a lamina or thin sheet or triangular plate is two-thirds of the distance of the median from the corresponding point. And this can be found by suspending any of the objects freely from two to three points.
For instance, the C.G of a rigid body in the figure below is the single point through which the weight of the body is considered to act.

The center of mass of an object is sometimes called its center of gravity. However, the center of mass is defined independently of any gravitational effect.
Centre of mass of an object is the point where the total mass appears to act.
If the distribution of masses and gravitational field strength (g) remains constant on all part of the object, the CG will coincide with the CM of the object.
Example on centre of gravity
A man of weight 600 N stands at the end of a uniform wooden plank, which is pivoted as shown in the diagram. What is the weight of the wooden plank?
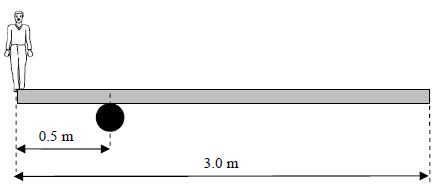
Solution
The CG of the plank is roughly at the midle since it is a uniform wooden plank. Therefore, the distance of the weight of the plank is 1.5m from the man.
Sum of clockwise momnet = sum of anticlockwise moment
w x 1 = 600 x 0.5 (the moment is taking from the pivot)
w = 300N
To view more example, click here
