How To Solve Questions On Equilibrium Of Forces
Question 1
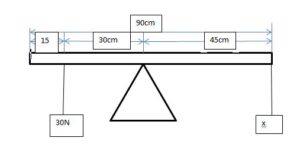
A 90cm uniform lever has a load of 30N suspended at 15cm from one of its ends. If the fulcrum is at the centre of
gravity, the force that must be applied at its other end to keep it in horizontal equilibrium is{UME 2003 Type 9}
A. 15N B. 20N C. 30N D. 60N.
Solution
sum of clockwise moment = sum of anti-clockwise moment
x * 45 = 30 * 30
45x = 900
x = 900 / 45
x = 20N
B is the correct option
Question 2
A 100kg box is pushed along a road with a force of 500N. If the box moves with a uniform velocity, the coefficient of
friction between the box and the road is{UME 2004 Type S}
A. 0.5 B. 0.4 C. 1.0 D. 0.8
solution
F – fr = ma
since it moves with a uniform velocity acceleration = 0
F = fr
F = μR
μ is the coefficient of friction
F is the force applied
R is the normal reaction which is equal to the weight = mg = 100*10 = 1000N
μ = F/R = 500 / 1000 = 0.5
A is the correct option
Question 3
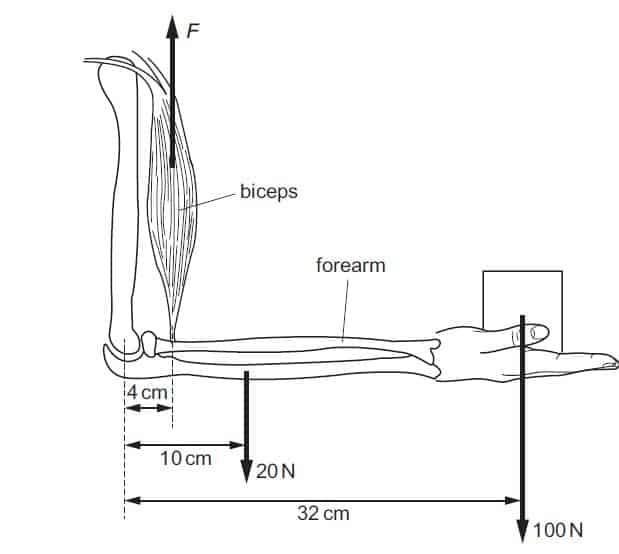
A man holds a 100 N load stationary in his hand. The combined weight of the forearm and hand is
20 N. The forearm is held horizontal, as shown{cambridge may/june 2014 p11 ques 12}
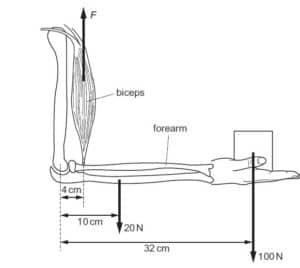
What is the vertical force F needed in the biceps?
A 750 N B 800 N C 850 N D 900 N
Solution
moment of a force = force x perpendicular distance
Sum of clockwise moment = sum of anti-clockwise moment
the 100N load will make a clockwise direction
the 20N combined weight of the hand and forearm will make a clockwise direction
the force F in the biceps will make anti-clockwise direction
F*4 = 20*10 + 100*32
4F = 200 +3200
4F = 3400
f = 3400/4
F = 850N
C is the correct option
Click here to read short note on forces
Question 4
A uniform plank AB of length 5.0 m and weight 200 N is placed across a stream, as shown below
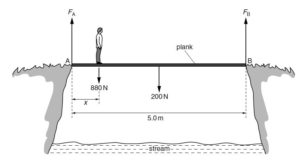
A man of weight 880 N stands a distance x from end A. The ground exerts a vertical force FA on the plank at end A and a vertical force FB on the plank at end B.
As the man moves along the plank, the plank is always in equilibrium.{cambridge may/jun 2014 p21 q3}
The man stands a distance x = 0.50 m from end A. Use the principle of moments to
calculate the magnitude of FB.
Solution
sum of clockwise moment = sum of anti-clockwise moment
taking your moment about FA
since it is a uniform plank, the weight of the plank will be at the mid-point of the plank
FB will make a anticlockwise direction
the man will make an clockwise direction
the weight of the plank will make clockwise direction
FB*5 = 200*2.5 +880*0.5
5FB = 500 +440
5FB = 940
FB = 940 / 5
FB = 188N
Question 5
A block of mass 2.0 kg is released from rest on a slope. It travels 7.0 m down the slope and falls a vertical distance of 3.0 m. The block experiences a frictional force parallel to the slope of 5.0 N.{cambridge may/june 2011 p11 que15}

What is the speed of the block after falling this distance?
A 4.9 m s–1 B 6.6 m s–1 C 8.6 m s–1 D 10.1 m s–1
Solution
mgsinθ – fr = ma
sinθ = opposite / hypothenus = 3 /7
g = 9.81 ms-2
2*9.81*3/7 – 5 = 2*a
8.41 – 5 = 2a
3.41 = 2a
a = 3.41 /2
a = 1.7 ms-2
using
v2 = u2 + 2as
initially it is at rest so
u = 0ms-1
distance covered is 7m
v2 = 2*1.7*7
v2 = 23.86
find the square root of both sides
v = 4.9ms-1
A is the correct option
Read: Moment of force
