How to Solve Questions on Linear Expansivity

In this article, i will solve questions on linear expansivity, define area and cubic expansion. Linear expansivity is defined as the increase in length, of the unit length of the material for one degree temperature rise.
To solve any question on L.E:
- Write down the formula
- Write down the data given
- Understand what you are asked to find
- Make proper substitution
- Evaluate
Advantages and disadvantages
Advantages
- Used for making bimetallic strips, which are used in thermostats
- Removal of tight glass stopper
- Red-hot rivets in shipbuilding
- Expansion of metals is used in bimetallic thermometer
Disadvantages
- Expansion of railway lines
- Sagging of overhead wire
- Expansion of balance wheel or wrist-watch
- Cracking of glass cup when hot water is poured into the glass cup
- Expansion of metals or concrete bridges
Area Expansivity: The increase in the area of an object with temperature change is called superficial expansivity or area expansivity.
The superficial expansivity of a material is defined as,

Its value is twice that of L.E.
Cubic Expansivity: Increasing temperature usually causes an increase in volume for both solid and liquid materials.
The cubic expansivity of a solid is defined as
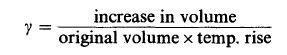
Its value is thrice that of L.E.
Steps on how to solve questions on linear expansivity
Question 1
What is meant by the statement: The linear expansivity of a solid is 1.0 x 10-5 k-1
Solution
The statement means that a unit length of the solid will expand in length by a fraction of 1.0 x 10-5 of the original per Kelvin rise in temperature.
Question 2
A wire of length 100.0m at 300C has a L.E of 2 x 10-5K-1. Calculate the length of the wire at a temperature of -100C {UTME 2013}
A. 99.92m B. 100.08m C. 100.04m D. 99.96m
Solution
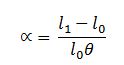
l1 = new length
l0 = original length
Q = temperature change
0.00002 = change in length / 100(30-(-10))
0.00002 = change in length / 100*40
0.00002*4000 = change in length
change in length = 0.08
change in length = 100 – x
x = 100 – 0.08 = 99.92m
A is the correct option
Question 3
Two metals P and Q are heated through the same temperature difference. If the ratio of the L.E of P to Q is 2: 3 and the ratio of their lengths is 3:4 respectively, the ratio of the increase in lengths of P to Q is {UTME 2012}
A. 1 : 2 B. 2 : 1 C. 8 : 9 D. 9 : 8
Solution
Temperature difference =( L.E * length)/increase in length
For metal P,
Qp = (L.E * length)p/increase in length p
For metal Q,
Qq = ( L.E * length q)/increase in length q
( linear expansivity * length)p/increase in length p = ( L.E * length q)/increase in length q
increase in length of p:increase length q = ( L.E * length)p / ( L.E * length q)
increase in length of p:increase length q = 2/3 *3 /4 = 6 / 12 = 1:2
A is the correct option
Question 4
A metal of volume 40cm3 is heated from 300C to 900C, the increase in volume is {UTME 2011}
A. 0.40cm3 B. 0.14cm3 C 4.00cm3 D. 1.20cm3.
[L.E of the metal= 2.0 x 10-5K-1]
Solution
cubic expansivity = 3* L.E = 3 * 0.00002 = 0.00006
0.00006 = increase in volume / 40*(90 – 30)
0.00006 = increase in volume / 40*60
increase in volume = 0.00006*2400 = 0.144cm3
B is the correct answer.
Question 5
A blacksmith heated a metal whose cubic expansivity is 6.3 x 10-6K-1. The area expansivity is {UTME 2007}
A. 6.3 x 10-6K-1 B. 4.2 x 10-6K-1 C. 2.1 x 10-6K-1 D. 2.0 x 10-6K-1
Solution
cubic expansivity = 3* L.E
0.0000063 = 3* L.E
L.E = 0.0000063/3 = 0.0000021
Area expansivity = 2*0.0000021 = 0.0000042
B is the correct option
Question 6
Calculate the length which corresponds to a temperature of 20^0C if the ice and steam points of an ungraduated thermometer are 400 mm apart
A. 80mm
B. 20mm
C. 30mm
D. 60mm
Solution
ice point = lower fixed point = 0^oC
steam point = upper fixed point = 100^oC
(100 -0)/(20 -0) = 400/(x – 0)
100/20 = 400 / x
20*400 = 100x
x = 8000/100
x = 80mm
A is the correct option
Question 7
A steel bridge is built in the summer when its temperature is 35.0°C. At the time of construction, its length is 80.00m. What is the length of the bridge on a cold winter day when its temperature is -12.0°C? (L.E of steel is 1.2 x10^-5)
Solution
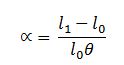
initial length = 80 m
initial temperature = 35.0°C
final length = ?
final temperature = -12.0°C
Change in temperature = final – initial = -12-35 = -47.0°C
let the change in length = x
o.oooo12 = x/80(-47)
x = 0.000012*80*(-47) = -0.04512 m
note
x = final length – initial length
-0.04512 = final length – 80
final length = 80 -0.04512 = 79.95488 m
The length of the bridge on a cold winter day = 79.95488 m
Question 8
A copper rod whose linear expansivity =1.70×10^-5°c is 20cm longer than an aluminum rod whose L.E =2.20×10^-5°c. How long should the copper rod be if the difference in their length is to be independent of temperature?
Solution
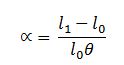
For copper,
L.E of copper = x
change in length of cooper = y
the original length of copper = c
temperature change = t
x = y/(c*t)
For aluminum,
linear expansivity of aluminum = a
change in length of aluminum = b
the original length of aluminum = d
temperature change = r
a = b/(d*r)
According to the question, copper is 20cm longer than an aluminum rod, i.e., c = d + 0.2
y/t = x*c = x*(d+0.2) = 1.70×10^-5*(d+0.2)
b/r = a*d = 2.20×10^-5*d
note, y/t = b/r since the difference in length is independent on temperature
2.20×10^-5*d = 1.70×10^-5*(d+0.2)
d = 1.7/2.2 * (d+0.2)
d = 0.7727d + 0.1545
d-0.7727d = 0.15
0.2273d = 0.1545
d = 0.68m
c = d + 0.2 = 0.68 +0.2 = 0.88m
Question 9
A metal of volume 40cm3 is heated from 300C to 900C; the increase in volume is
A. 0.40cm3 B. 0.14cm3 C 4.00cm3 D. 1.20cm3.
[L.E of the metal = 2.0 x 10-5K-1]
Answer
Volume expansivity = 3 x Linear expansivity = 3 x 2.0 x 10-5K-1 = 6.0 x 10-5K-1
Increase in volume = x
V.E = (x) / (initial volume x temp rise)
6.0 x 10-5 = x / (40 x (90 – 30))
X = 6.0 x 10-5 x 40 x 60 = 14400 x 10-5 = 0.144 cm3
Question 10
A blacksmith heated a metal whose cubic expansivity is 6.3 x 10-6K-1. The area expansivity is
A. 6.3 x 10-6K-1 B. 4.2 x 10-6K-1 C. 2.1 x 10-6K-1 D. 2.0 x 10-6K-1
Answer
The cubic expansivity = 6.3 x 10-6K-1
Recall that
cubic expansivity = 3 x L.E
Therefore,
L.E = (6.3 x 10-6)/3 = 2.1 x 10-6
Area expansivity = 2 x L.E = 2 x 2.1 x 10-6 = 4.2 x 10-6 K-1
Recommended: Solved questions on other topics in physics
