How To Calculate And Solve Questions On Resistivity
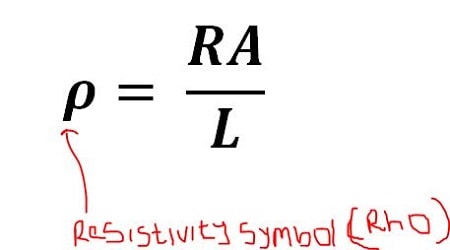
In this article, I will define; give the value of the resistivity of some materials, and how to solve some questions on it.
The resistance R is proportional to the length L and inversely proportional to the cross-sectional area A, with a proportionality factor called the resistivity of the material.
Note: In a metal resistivity increases with temperature.
The symbol is given below,
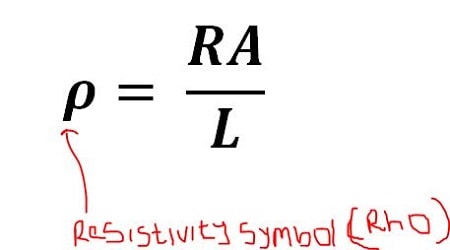
The Unit is Ωm
It is important to note that its reciprocal is conductivity.
Table of Contents
Difference between Resistivity and Resistance
Resistivity is a property of a material, independent of the shape and size of the specimen, while resistance depends on the size and shape of the specimen or device, as well as on its resistivity.
It then means that the resistance of a wire depends on resistivity, length, area of the wire. Also resistance depends on the temperature.
Resistivity of some materials at room temperature
| Materials (Metals) | (Ωm) |
| Silver | 1.47 x 1028 |
| Copper | 1.72 x 1028 |
| Gold | 2.44 x 1028 |
| Aluminum | 2.63 x 1028 |
| Tungsten | 5.51 x 1028 |
| Steel | 20 x 1028 |
| Lead | 22 x 1028 |
| Mercury | 95 x 1028 |
| Nichrome alloy | 100 x 1028 |
How to calculate resistivity
The parameters you must have in order to calculate include
- Resistance of the material
- Length of the material
- And the cross-sectional area of the material which is
Few Questions
(1) A wire of 5Ω resistance is drawn out so that its new length is two times the original length. If the resistivity of the wire remains the same and the cross sectional area is halved, the new resistance is
A. 40Ω B. 20 Ω C. 10 Ω D. 5 Ω
(2) A wire P has half the diameter and half the length of a wire Q of similar material. The ratio of the length of the resistance of P to that of Q is?
(3) The resistance of a 5m uniform wire of cross-sectional area 0.2 x 10-6 is 0.425 ohms. What is the resistivity of the material of the wire?
Answers
Q1
Since the ‘resistivity’ is the same
(R1A1)/(L1) = (R2A2)/(L2)
L2 = 2 X L1, A2 = 0.5 x A1
Then,
(5 X A1)/(L1) =( R2 X 0.5A1)/(2L1)
R2 = (5 X A1 X 2L1) / L1 X 0.5A1 = 10/0.5 = 20 ohms
Q2
Diameter of P = 0.5 x diameter of Q
Length of P = 0.5 x length of Q
‘Resistivity’ of P = ‘Resistivity’ of Q
Cross sectional area =
RpAp/Lp = RqAq/Lq
Rp(dp)2/Lp = Rq(dq)2/Lq
Rp(0.5dq)2/0.5Lq = Rq(dq)2/Lq
0.5Rp = Rq
Rp/Rq = 1/0.5 = 2:1
Q3
‘Resistivity’ = RA/L = (0.425 x 0.2 x 10-6) / 5 = 1.7 x 10-8
Recommended: Why Ammeter is connected in series and Voltmeter in parallel
a battery of 4 cell each of emf 1.5v and internal resistance 1.0ohm is connected to 1.0ohm resistor in series with a parallel combination of 2ohm resistor (a) draw the circuit diagram (b)calculate (I)combined external resistance (II)current in the circuit (III)lost voltage in the battery (IV)the current I of the 2ohm resistor