How to Calculate and Solve Potential Divider Problems
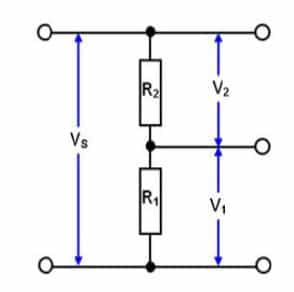
A potential divider circuit is arranged in such a way to get an output voltage from a battery of particular e.m.f.
For a potential divider, the current through the each resistor is the same because they are arranged in series.
Potential Divider derivation

Using Ohms law,
The effective resistance is = R1 + R2
Vin = IR
I = Vin/ (R1 + R2 )
The Voltage across R1 will be,
V1 = IR1
Since I = Vin/ (R1 + R2 )
V1 = Vin/ (R1 + R2 ) x R1
V1 = R1/(R1 + R2 ) x Vin
For voltage across R2
V2 = R2/(R1 + R2 ) x Vin
Uses of Potential divider
The circuits are often used in electronic circuits. They are useful when a sensor is connected to a processing circuits.
Temperature sensor
A common example of a sensing system is a temperature sensor in a thermostat, which uses a thermistor. The thermistor is then used in a potential divider as the diagram below. In the diagram, the potential difference is divided between the resistor and the thermistor. As the temperature rises, the resistance of the thermistor decreases, so the potential difference across it decreases and the potential difference across the resistor increases as the temperature increases.
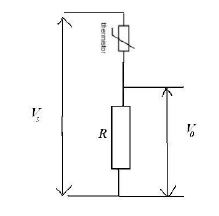
How to calculate in Potential divider circuits
The first thing that must be done is to write down the formula
Vout = R2/(R1 + R2 ) x Vin
Then look at the question to know what you are asked to calculate.
Example 1
The diagram shows a potential divider circuit. The voltmeter has infinite resistance and the battery has negligible internal resistance.
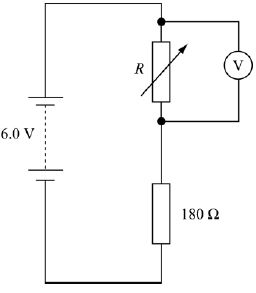
The variable resistor is set on its maximum resistance of 200 Ω. Calculate the voltmeter reading.
Solution
V = 200 /(200 + 180) x 6
V = (200/380) x 6 = 3.16 v
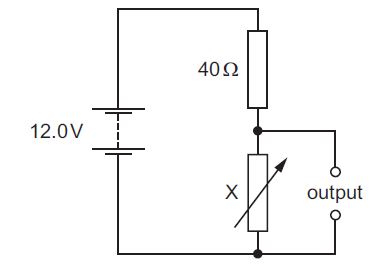
Example 2
In the circuit shown, X is a variable resistor whose resistance can be changed from 5.0 Ω to 500 Ω. The e.m.f. of the battery is 12.0 V. It has negligible internal resistance.
What is the maximum range of values of potential difference across the output?
A 1.3 V to 11.1 V
B 1.3 V to 12.0 V
C 1.5 V to 11.1 V
D 1.5 V to 12.0 V
Solution
Vout = R2/(R1 + R2 ) x Vin
The minimum resistance in variable resistor is 5Ω
Vout = 5/(5 + 40) x 12 = 1.3 v
The maximum resistance is 500Ω
Vout = 500/(500 + 40) x 12 = 11.1 v
The correct answer is A
Recommended: How to calculate and solve questions on resistivity
