Moment Of Force With Calculation
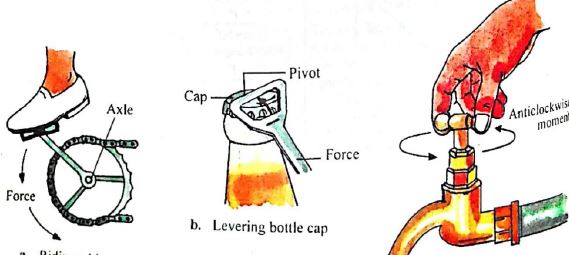
Whenever we open a door, the force we put on the door handle exerts a turning effect about the hinges. When we ride a bicycle the push we exert on the pedals with the feet produces a turning effect which causes the wheels to rotate. When we turn a tap, tighten a nut with a spanner or screw driver, we are exerting a turning force and producing a turning effect about a point or along an axis. Such a turning effect brought about in each case is called the moment of force.
Two factors are involved in each case;
- The magnitude of the force applied
- The perpendicular distance of its line of action from the axis or pivot about which the turning effect is felt or exerted

The moment of a force about a point (or axis) C is the turning effect of the force about that point. It is equal to the product of the force and the perpendicular distance of its line of action from the point C.
Moment = force x perpendicular distance of pivot to the line of action of the force. Since force is in Newtons (N) and distance is in meters, the S.I unit of moment is expressed in Newton-metre (Nm). It is a vector quantity.
The principle of moments states that if a body is in equilibrium, then the sum of the clockwise moments about any point on the body is equal to the sum of the anticlockwise moments about the same point.
Read: Note on forces and inclined plane
Calculating Weights
Centre of Gravity of a body is defined as the point through which the line of action of the weight of the body always passes irrespective of the position of the body. It is also the point at which the entire weight of the body appears to concentrate.
Every object has a centre of gravity
- A uniform rod has its C.G at the midpoint of the length of the rod. The weight of the rod acts through G
- The C,G, of a uniform circular plate it at its centre
- The C.G. of a uniform circular ring is at its centre
For instance, a metre rule is supported at its centre of gravity by a knife edge, a known weight W2 and an unknown weight W1 are suspended from to either side of the rule using the weight hangers. The position of one weight hanger and the second weight hanger is fixed such that the rule is in equilibrium. Then measure the distance d1 and d2 of the two weight hangers from the centre of the rule accurately.
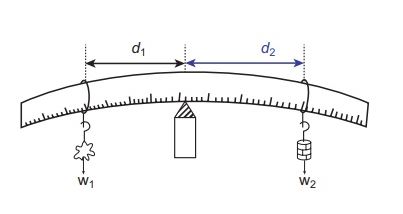
Clock wise moment by unknown weight = W1 × d1
Anticlockwise moment by known weight = W2 × d2
W1 × d1= W2 × d2
w1 w2
Unknown weight = W1= (W2 × d2 ) /d1
Determine the Moment of Force F About Point a
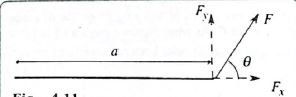
Resolve F into its vertical and horizontal components.
Vertical component Fy = F sinq
Horizontal component Fx = Fcosq
The moment of Fx about A is zero because its line of action passes through A. moment of Fy about A is Fy x a = F sin q x a = FAsin q
Example
Weights of 20N and 50N are hung on a light beam as shown below. Find the moments of forces about O
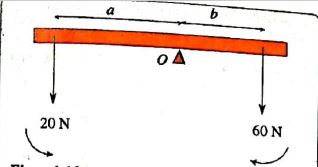
Moment of 20 N force about O = 20 x a = 20a Nm
Moment of 60 N force about O = 60 x b = 60b Nm
