How to solve questions on capacitance of capacitor for Cambridge A level and UTME
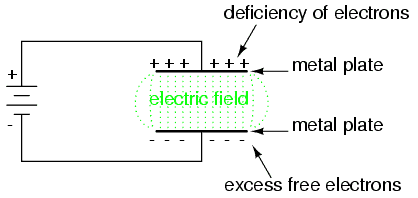
How to solve questions on capacitance of capacitor for Cambridge A level and UTME
Question 1
Three capacitors, each of capacitance 48 μF, are connected as shown in Fig below
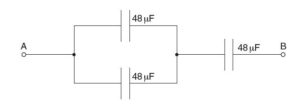
(a) Calculate the total capacitance between points A and B.
(b) The maximum safe potential difference that can be applied across any one capacitor is 6 V. Determine the maximum safe potential difference that can be applied between points A and B.{cambridge A level oct/nov 2014 p43}
solution
for parallel arrangement
c = c1 + c2
c = 48 + 48 = 96uf
96uf is in series with the third 48uf
1/c = 1/c1 + 1/c2
1/c = 1/96 + 1/48
1/c = 3/96
c = 32uf
(b)
In parallel same volatage across the capacitors, while in series same charge across the capacitors
The total charge flowing through the circuit is
C = Q/V
48 x 10^-6 = Q/6
Q = 48*6 x 10^-6 = 288 x 10^-6 c
p.d across the capacitor connected in parallel will be
C = Q/V
96 x 10^-6 = 288 x 10^-6 / V
v = 288 / 96 = 3v
the maximum safe potential difference that can be applied between points A and B = 3 + 6 =9v
or
p.d. across parallel combination is one half p.d. across single capacitor C1
total p.d. = 9 V
Question 2
The combined capacitance between terminals A and B of the arrangement shown in Fig below is 4.0 μF.
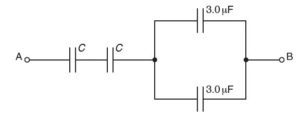
Two capacitors each have capacitance C and the remaining capacitors each have capacitance 3.0 μF. The potential difference (p.d.) between terminals A and B is 12 V.
(i) Determine the capacitance C
(ii) Calculate the magnitude of the total positive charge transferred to the arrangement
(iii) Use your answer in (ii) to state the magnitude of the charge on one plate of
1. a capacitor of capacitance C,
2. a capacitor of capacitance 3.0 μF.{cambridge Alevel may/june p42}
solution
(i)
3.0 μF and 3.0 μF are in parallel
c= 3 + 3
c = 6μF
6μF is in series with c and c
1/Ct = 1/6 + 1/c + 1/c
1/4 = 1/6 + 1/c + 1/c
1/4 – 1/6 = 2/c
1/12 = 2/c
C =24uf
(ii)
The potential difference between terminal A and B is 12v
Total capacitance = total charge / total p.d
4 × 10^-6 = Q / 12
Q = 48 × 10^-6 c
(iii)
The charge on capacitor c is the same as the total charge in the arrangement = 48 × 10^-6 c
The charge on 3uf capacitor will be,
Firstly we need to know the p.d across the two capacitors arranged in parallel.
C = Q/v
6uf is the combined capacitance of the two capacitors
6 × 10^-6 = 48 × 10^-6 / v
V = 48/6 = 8v
The charge on the 3uf capacitor will be
3 × 10^-6 = Q/8
Cross multiply
Q = 24 × 10^-6 c
Question 3
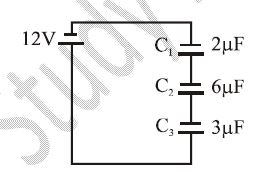
The diagram shows three capacitors C1, C2 and C3 of capacitances 2 μF, 6 μF and 3 μF respectively. The potential
differences across C1, C2 and C3 respectively are{UTME 2001}
A. 6V, 2V and 4V.
B. 6V, 4V and 2V.
C. 2V, 6V and 4V.
D. 4V, 6V and 2V.
Solution
The arrangement are in series, so the effective capacitance
1 / c = 1/ C1 + 1/ C2 + 1/ C3
1 / C = 1/ 2 + 1/6 + 1/ 3
1 / C = (3+1+2)/6
1/ C = 1/1
c = 1 μF
note that,
Q = CV
Q = 1*12 =12 C
For series arrangement the same charge will flow through the capacitors
on C1,
12 = 2V
V = 6v
on C2,
12 = 6V
V = 2 v
on C3,
12 = 3V
V = 4 v
The potential difference = 6v, 2v, 4v
A is the correct option
Question 4
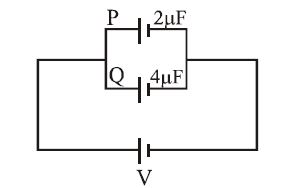
The diagram above shows two capacitors P and Q and capacitances 2μF and 4μF respectively connected to
a d.c. source. The ratio of energy stored in P to Q is{UTME 2001}
A. 1 : 2 B. 2 : 1 C. 4 : 1 D. 1 : 4
Solution
The arrangement is parallel, the implication of that is, the same voltage will be supplied across the capacitors
E = 1/2 CV^2
Ep = 1/2 *2*V^2 = V^2
Eq = 1/2*4*V^2 = 2 V^2
Their ratio = Ep /Eq = V^2 / 2V^2 = 1/2
A is the correct answer
Recommended: short note on capacitance of a capacitor
