How to solve questions on Measurement and Kinematics for Cambridge A level
The two questions are cambridge may/june 2012 p21
Q1
The volume V of liquid that flows through a pipe in time t is given by the equation
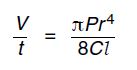
where P is the pressure difference between the ends of the pipe of radius r and length l.
The constant C depends on the frictional effects of the liquid.
Determine the base units of C.
solution
The base unit of pressure is
![]()
the base unit for radius = m
the base unit for length = m
volume = m^3
t = s
the first thing to do is to make C the subject of the equation
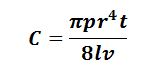
Substitute all the base units
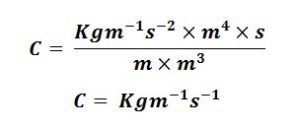
Q2
A ball is thrown vertically down towards the ground with an initial velocity of 4.23 m s–1. The
ball falls for a time of 1.51 s before hitting the ground. Air resistance is negligible.
(a) (i) Show that the downwards velocity of the ball when it hits the ground is 19.0 m s–1.
(ii) Calculate, to three significant figures, the distance the ball falls to the ground.
(b) The ball makes contact with the ground for 12.5 ms and rebounds with an upwards
velocity of 18.6 m s–1. The mass of the ball is 46.5 g.
(i) Calculate the average force acting on the ball on impact with the ground
Solution
v = u + at
u = 4.23 ms-1
t = 1.51 s
a = 9.81
v = 4.23 + 1.51 *9.81
v = 19.04 ms-1
ii
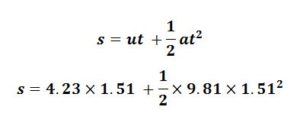
s = 17.57 m
b

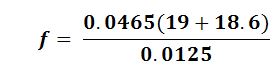
F = 140 N
A ball of mass 400 g is thrown with an initial velocity of 30.0 m s–1 at an angle of 45.0° to the
horizontal, as shown in fig below
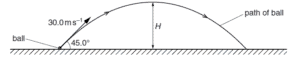
Air resistance is negligible. The ball reaches a maximum height H after a time of 2.16 s.
(i) Calculate
1. the initial kinetic energy of the ball,
2. the maximum height H of the ball
cambridge past que may / jun 2014 p22 q4
Solution
Ek = 1/2 m v2
m = 400g = 0.4kg
v = 30ms-1
Ek = 1/ 2 * 0.4 * 30 ^2 = 180 J
To calculate the maximum
v2=u2– 2as
v = 0
u is the vertical component of the velocity = usinθ = 30 sin 45 = 21.21 ms-1
s = 21.21^2 / 2* 9.81 = 22.94m
2.
A ball is thrown from a point P, which is at ground level, as illustrated in figure below
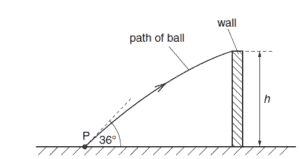
The initial velocity of the ball is 12.4 m s–1 at an angle of 36° to the horizontal.
The ball just passes over a wall of height h. The ball reaches the wall 0.17 s after it has been
thrown.
Assuming air resistance to be negligible, calculate
(i) the horizontal distance of point P from the wall,
(ii) the height h of the wall.
cambridge past que oct / nov 2010 p22 que 2
Solution
the horizontal distance is
v = d/t
v = ucosθ = 12.4 cos 36 = 10.03 ms-1
d = vt = 10.03 * 0.17 = 1.7 m
the heignt h
s = ut – 1/2 a t2
the u here is the vertical component of the initial velocity usinθ = 12.4 sin 36 = 7.29 ms-1
s = 7.29 * 0.17 – 1/2 * 9.81 * 0.17^2 = 1.24 – 0.14 = 1.1 m
3.
An object is projected from a height of 80m above the ground with a velocity of 40ms-1 at an angle of 30o to the horizontal. The time of flight is
A. 16s B. 10s C. 8s D. 4s
[g = 10ms-2]
Solution
T = 2usinθ / g
T = 2 * 40 * sin 30 / 10
T = 40 / 10
T = 4 s
