Quantitative Reasoning is a measures a person’s ability to use mathematical or analytical skills in order to solve problems.
Here, I will be solving some examples on quantitative reasoning for primary 3, 4, and 5 pupils.
Example 1
Solution
One good thing about quantitative reasoning is that it helps you to think deeply in order to generate the right answer.
The technique used in the above example follow this pattern;
(2*3) – 5 = 1
(16*3) – 5 = 43
(27*3) – 5 = 76
(40*3) – 5 = 115
Use this format to solve the remaining question
(10*3) – 5 = 25
(15*3) – 5 = 40
(33*3) – 5 = 94
(54*3) – 5 = 157
Example 2
Solution
The format to solve this particular question is discussed below;
139 * 3 = 417
258 * 2 = 516
In order to solve the first question,
113 * 5 = 565
Therefore, 6 will be in the box
Example 3
Solution
(9*4) divided by square root of 9 = 36/3 = 12
(36*5) / square root of 36 = 180/6 = 30
(64*2)/ square root of 64 = 128/8 = 16
Example 4
Solution
The numbers in COLUMN must be the same in the ROW
For ROW 1, the numbers are 1, 2, 3, 0, 1
For COLUMN 1, the numbers are, 1, 2, G, 0, T
The G is 3
The T is 1
So use the same method for the rest.
Example 5
Solution
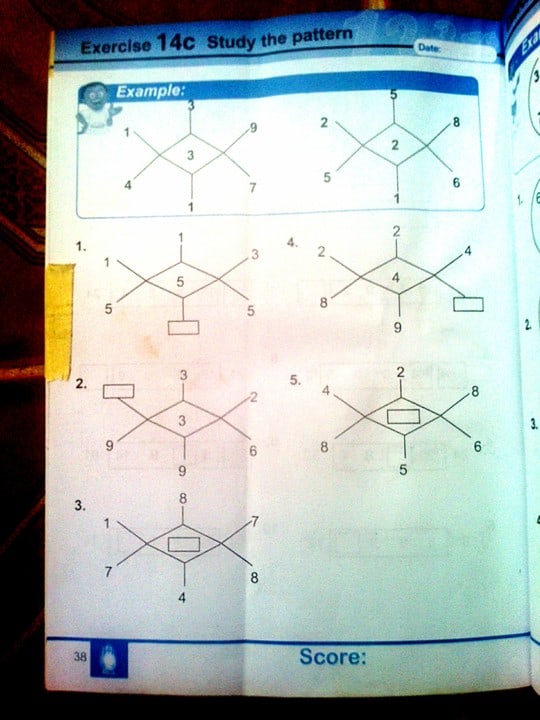
The first sample question: take the 2 and 2 in the square boxes to be 22, multiply the 3 and 6 in the triangle boxes together. then subtract i.e. 22-(6*3) = 4 in the circular box
2nd sample: 18-(2*5) = 8
sample 3: 22-(7*3) = 1
Use this approach to solve question 6-10 of the diagram
Example 6
Solution
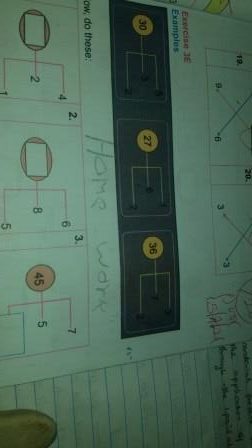
From the samples given, if you add the first two columns together, it will give the third column.
1st example, 4118 + 5420 = 9538
2nd example, 1257 + 3482 = 4739
Also, if you subtract the first column from the second column, it will give you the fourth column.
sample 1, 5420 – 4118 = 1302
sample 2, 3482 – 1257 = 2225
Use this same method to solve question 1-5 of the diagram
Example 7
Solution
If you look at the first example, add the left hand side together (7+5+4+3 = 19) and the right hand side (9+12+15+21 =57). So if you multiply the sum of the left hand side which is 19 x 3 you will get the sum of the right hand side which is 57
The same for the second example , left hand side 12+5+13+8 = 38, the right hand side is 24+36+15+39 = 114. if you multiply the 38 x 3 = 114
In summary if you add the numbers in the left hand side and multiply by 3, you will get the sum of the numbers on the right hand side.
Example 8
solution
Example 9
Solution
(34/2) + 6 = 23
(49/2) + 6 = 30 1/2
(62/2) + 6 = 37
(76/2) + 6 = 44
For the first sample, the format is
(2+2+1+3)*3=24
(0+4+3+6)*3 =39
(4+1+2+4)*3=33
You add all the numbers at the edge of the diagram and multiply by 3
For the second sample,
2*8=12+4=16
5*9=17+28=45
7*7=25+24=49
Example 11
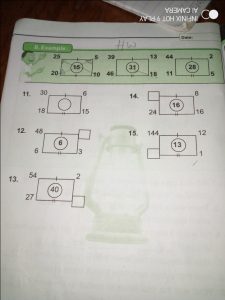
From the example, 25/5 = 5, 20-10 = 10
Then add the two answers 5+10 = 15 that is the number in the middle
For the second one, 39/13 = 3, 46-18 = 28, so 28+3 = 31
For the third one, 44/2 = 23, 11-6 = 5, so 23+5 = 28
Example 12
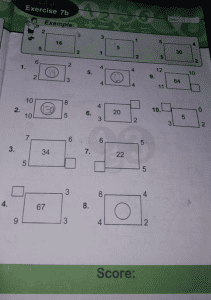
For sample 1, (2^2 + 5^2) -(3^2 + 2^2) = 16
(4 +25) – (9+4) = 16
29-13 = 16
For sample 2, (3^2 + 1^2) – (1^2 + 2^2) = 5
(9 + 1) – (1 + 4) = 5
10 – 5 = 5
For sample 3, (5^2 + 5^2) – (4^2 + 2^2) = 30
(25 + 25) – (16 + 4) = 30
50 – 20 = 30
So, you can use the above approach to solve the remaining questions.
If you have any question on quantitative reasoning, you can link me up on Twitter. Also, if you need quantitative reasoning common entrance past question for your child and private tutoring send a whatsapp message to 09059059123.
Recommended: How to have good grade in math
