Notes on ideal gases for Cambridge A level and UTME
Notes on ideal gases for Cambridge A level and UTME
An ideal gas is one that obeys the gas laws, and equation of state for ideal gas, at all temperature, pressure and volume. This means Ideal gas obeys
pV = nRT
P = Pressure
V = Volume
T = Temperature
R = universal gas constant
n= number of moles
Infer from a Brownian motion experiment the evidence for the movement of molecules
Brownian motion: random movement of small particles caused be bombardment of invisible molecules
- Smoke (oil droplets) are seen to move randomly
- This motion is evidence that the air particles are also moving randomly and colliding with the smoke droplets
- The air particles cannot be seen but their motion can be understood by the smoke droplets which can be seen
Kinetic theory of gases
- The attraction between molecules is negligible
- The volume of the molecules is negligible compared with the volume occupied by the gas
- The molecules are like perfectly elastic spheres
- The duration of a collision is negligible compared with the time between collisions
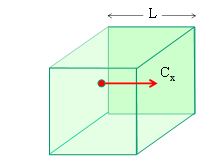
Explain how molecular movement causes the pressure exerted by a gas and hence deduce the relationship p = 1/3Nm/V < c 2 >
(N = number of molecules)

- Consider a cube of space with length L
- Consider a particle moving in one dimension x with velocity cx
- When the particle collides with the wall its velocity is reversed so its change in momentum is equal to…
- Dpx = 2mcx
- The time between collisions with each wall of the cube is equal to…
- Time between collisions = 2L / cx
- The rate at which momentum is transferred to the wall is…
- Rate of change of momentum = 2mcx / (2L/cx) = mcx 2 / L
- If there are N particles in the cube the total force is…
- Total force = Nmcx 2 / L
- Pressure is force over area so pressure is…
- Pressure on one wall is Nmcx 2 / L3
- L3 is the volume so…
- Pressure = Nmcx 2 / V
- The average of cx 2 can be written as < cx 2>
- As all directions, x, y and z can be considered equal
- < cx 2> = 1/3< c 2>
- Hence
- P = 1/3Nm<c 2> / V
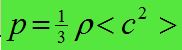
- p(rho) = density of gas
- <c²> = mean square speed
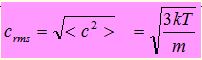
It should be carefully noted that the pressure p of the gas depends on the “mean square” of the speed. This is because
- The momentum change at a wall is proportional to the speed
- The time interval before this change is repeated is inversely proportional to the speed
Compare pV = 1/ 3 Nm < c 2 > with pV = NkT and hence deduce that the average translational kinetic energy of a molecule is proportional to T.
- The average translational Ek of the particles can be expressed as …
- <Ek> = 1/2m< c2>
- Combining with P = 1/3Nm<c 2> / V we get….
- pV = 2/3N(1/2m< c2>) = 2/3N<Ek>
- Combining this with pV = NkT we get…
- pV = 2/3N<Ek> = NkT
- <Ek> =3/2kT
- Therefore, Temperature is proportional to Average translational kinetic energy
Note
R/N = K
K is the Boltzman’s constant
R is the molar gas constant
Recommended: Solved questions on gravitational field
