Notes on nuclear physics for Cambridge A level and UTME

Notes on nuclear physics for Cambridge A level and UTME

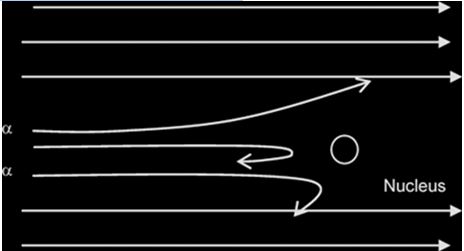
Rutherford alpha particle scattering experiment: Experimental evidence for nuclear atom:Results of an experiment where a beam of alpha particles is fired at a thin gold foil (about 1µm thick): where n= number of alpha particles incident per unit time.

Alpha particle are helium atom particles. He bombarded positive alpha particle on thin foil of gold approximately 8.6 x 10^-6 cm thick and took observations of the screen Zns which was behind the gold foil.

A gold foil was used because gold can be made into a very thin sheet or foil

Reasons why beta particle from a radioactive source would be inappropriate for this type of scateering experiment

1. beta particles have a range of energies
2. beta particles deviated by orbital electron
3. beta particle has very small size

Note

Change in Isotope of gold doesn’t affect deviation because deviation depends on charge on the nucleus or electrostatic repulsion i.e same charge since isotopes are element of the same proton number but different nucleon number, so no change in deviation

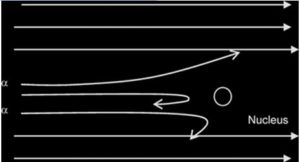
Observations

1. Most of the α-particles passed through the metal foil undeflected or deflected by(deviated through) very small angles less than 90
2.  A very small proportion was deflected by large angles more than 90°( some of these approaching 180°)

Conclusion

1. the nucleus occupies only a small proportion of the available space in comparism with atom size (i.e the atom is mostly empty space)
2. the nucleus is very small and heavy/dense/massive and +vely charged (since the positively-charged alpha particles are repelled/deflected).

 The energy conversion in the α-particle scattering experiment:

The kinetic energy of the incoming α-particle is converted to the electrical potential energy when it stops at the point of closest approach and turns around.

So  initial kinetic energy of α + nucleus(= 0) =  maximum electrical potential energy of both particles                                                                                           i.e

1/2m_α v_α² =  Q_α .Q_{N /}4πεr

where r is the distance( of closest approach) of α-particle to the nucleus,

Q_α = 2e,       and      Q_{N =} Ze  ,  Z is proton number

Reasonable estimates:

*Nuclear diameter ≈10^-15m …10^-13  to  10^-15 m                                                                                                                        *Atomic diameter ≈ 10^-10-m   …..10^-9  to  10^-11m

Nucleon:   A particle within the nucleus; can be either a proton or a neutron;they are subatomic particles.

Nuclide:   An atom with a particular number of protons and a particular number of neutrons

Proton number Z {old name: atomic number}: Number of protons in an atom

Nucleon number N {mass number}: Sum of number of protons and neutrons in an atom

Isotopes: are nuclei/atoms with the same proton number, but different nucleon/neutrons number

Density Calculation

Density = mass / volume

mass is mass of nucleus

v is the volume of nucleus

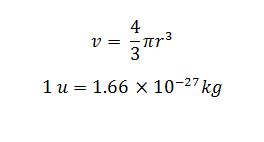
r is the radius of the nucleus

mass of a nucleus is measure in atomic mass unit because it is very small

Nuclear Energy

               Mass Defect                                                                                                                                          

Whenever a reaction results in a release of energy, there is an associated decrease in mass, called mass defect, which is converted to energy(in form of gamma radiation with c = 3.00 × 10⁸m/s).

The mass of a nucleus is always less than the total mass of its constituents (protons plus neutrons).

Mass  defect is this difference between the mass of a nucleus and the total mass of its individual nucleons,

i.e

Mass defect = (total)mass of nucleons ― (single)mass of nucleus

= Zm_p + (A – Z)m_n – Mass ofNucleus

Mass defect =  final mass – initial mass

Nuclear Binding Energy:

• This is energy that is required to completely separate the nucleons in a nucleus.

OR

The energy released (not  energy lost) when a nucleus is formed from its constituent nucleons

The Binding Energy per nucleon is a measure of the stability of the nucleus since it represents the average energy needed to remove a nucleon. The higher the binding energy, the more stable the nucleus and vice versa

Energy & Mass are Equivalent and inter-convertible.

Thus, Binding Energy, the energy released during nuclear reaction is

         E(J) = Mass defect(kg) × c²

Mass defect of a nucleus is the difference between the toatal mass of a separate necleus and the combined mass of the nucleus

         E = Increase/decrease in binding energy

                i.e  Energy released = total B.E after ― total B.E before

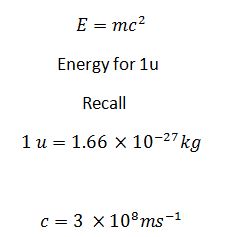
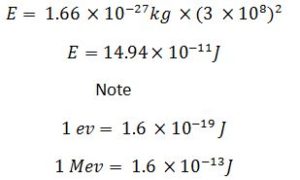
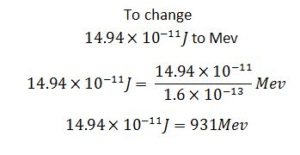
So

I u = 931Mev

         E(Mev) = 931Mev/u × Mass defect(u)   

         E = Binding energy per nucleon × nucleon number

if binding energy is:                                                                                                                                                       

+ve,nucleus is stable, energy released appears as k.e of products    

  ―ve, nucleus is unstable and will decay spontaneously, energy is needed to produce reaction    

Nuclear fission:

The disintegration of a heavy nucleus into two lighter nuclei of approximately same mass. Typically, the fission fragments have approximately the same mass and neutrons are emitted

Nuclear fusion:

The joining together of two light nuclei of nearly equal mass to form a heavy nucleus.

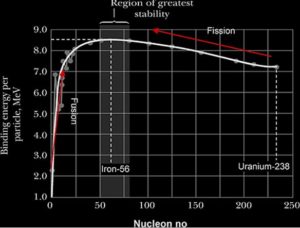
Radioactive decay:

Radioactivity is the spontaneous and random decay of an unstable nucleus, with the emission of an alpha or beta particle, with or without  the emission of a gamma ray photon.

Spontaneity:

*The emission is  unaffected (not speeded up or slowed down) by factors outside the nucleus,  e.g

1. chemical reactions(acids),
2. environmental factor/surrounding (heat, wind, cold, earth, pollution, weather)
3. all external factors.

Randomness:

*It cannot be predicted when the next emission will occur/which particular nuclei will decay next

*All nuclei have equal chance of decay i.e constant probability of decay per time of a nucleus

Exponential Decay curve

For a large number of a particular nuclei/species, the rate of decay is directly proportional to the number of parent nuclei present.

i.e                                         ― dN/dt  α  λ

dN/dt  =  ―λN                                         (Activity defined in Bq)

λ = +ve constant of proportionality/radioactive decay/disintegration constant in s^-1

where N= number of undecayed/active/parent nuclei at that instant/remaining.

 i.e the number of nuclei N remaining and/or activity after some time  t,  decreases exponentially.                                                                                          

              Units:     1Bq = 1disintegration per second,  1Ci = 3.7 ×10¹⁰s^-1

*Decay constant λ is defined as the probability of decay of a nucleus per (unit) time

*Activity is defined as the rate at which the nuclei are disintegrating/decay rate i.e number of decays per time (―ve…decreasing)

A = dN/dt = ― λN,      and          A₀ = λ N₀

Since number of undecayed nuclei ∝ Mass of sample,

Number of nuclei in sample = (Sample Mass / Mass of 1 mol) x N_A

Also, following the decay law,

N = N₀e^–λt ,             A = A₀e^–λt ,              C = C₀e^–λt

Half-life ,T_1/2      

  Half-life is defined as the (average) time taken for half the number {not: mass or amount} of undecayed nuclei in the sample to disintegrate,

or, the (average) time taken for the activity to fall to half of its original value.

T_½ = (ln2) / λ

                                                             or              T_1/2 = 0.6931/λ

Recommended: Question and answer on Nuclear for UTME