How to solve questions on oscillation for Cambridge A level
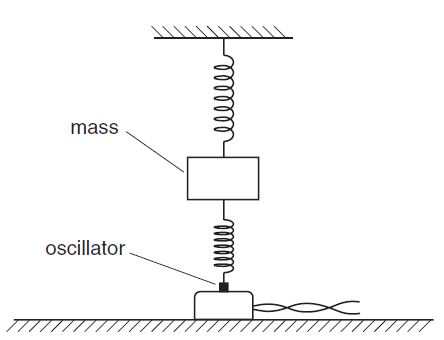
cambridge oct/nov 2006 p4
Q1
Two vertical springs, each having spring constant k, support a mass. The lower spring is
attached to an oscillator as shown below
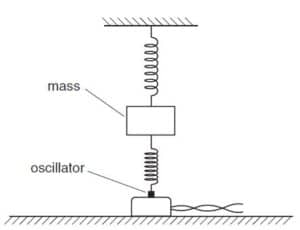
The oscillator is switched off. The mass is displaced vertically and then released so that it
vibrates. During these vibrations, the springs are always extended. The vertical acceleration
a of the mass m is given by the expression
ma = –2kx,
where x is the vertical displacement of the mass from its equilibrium position.
Show that, for a mass of 240 g and springs with spring constant 3.0Ncm–1, the
frequency of vibration of the mass is approximately 8Hz
Solution
mass = 240g = 0.24kg
k = 3.0 Ncm-1 = 300 Nm-1
ma = –2kx
![]() ……….i
……….i
0.24*a = -2* 300* x
a = -600x / 0.24
a = 2500x
substitute for a in equ i
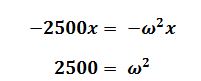
find the square root of both sides
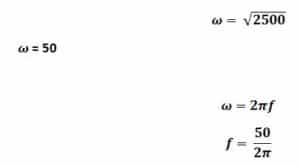
f = 8 Hz
The question is from cambridge may/june 2014 p41
A student investigates the energy changes of a mass oscillating on a vertical spring, as shown below
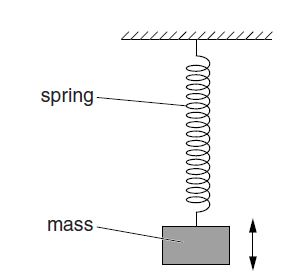
The student draws a graph of the variation with displacement x of energy E of the oscillation, as shown below
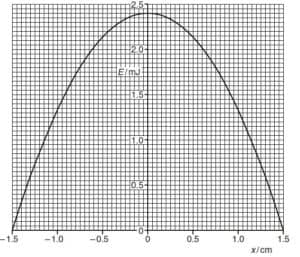
The student repeats the investigation but with a smaller amplitude. The maximum value of E
is now found to be 1.8 mJ.
Use graph above to determine the change in the amplitude
Solution
From the graph the maximum kinetic energy = 2.4 mJ
Change in Kinetic energy = 2.4 – 1.8 = 0.6 mJ
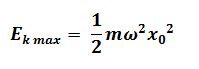
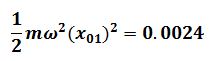
Amplitude = 1.5 cm = 0.015 m
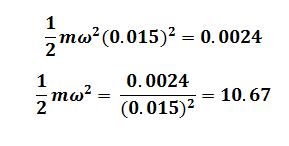
When the amplitude change maximum energy E is 1.8m J
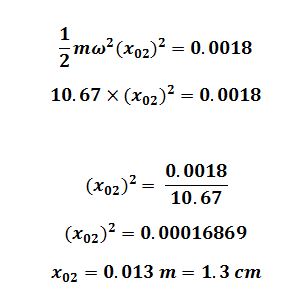
Change in Amplitude = 1.5 cm – 1.3 cm
change in amplitude = 0.2 cm
