How to solve questions on dynamics for CIE A Level Physics
This article is intended to help students who finds it difficult to solve questions on dynamics. Below are some questions on dynamics and steps on how to answer them.
Question 1
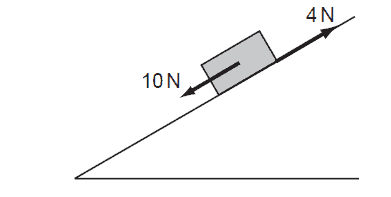
A brick weighing 20 N rests on an inclined plane. The weight of the brick has a component of 10 N
parallel with the plane. The brick also experiences a frictional force of 4 N.
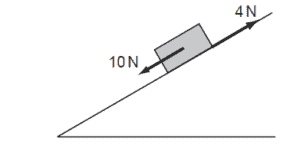
What is the acceleration of the brick down the plane? Assume that the acceleration of free fall g is
equal to 10 m s–2.
Question 2
The diagram shows a barrel suspended from a frictionless pulley on a building. The rope
supporting the barrel goes over the pulley and is secured to a stake at the bottom of the building
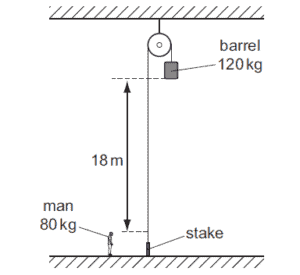
A man stands close to the stake. The bottom of the barrel is 18 m above the man’s head. The
mass of the barrel is 120 kg and the mass of the man is 80 kg.
The man keeps hold of the rope after untying it from the stake and is lifted upwards as the barrel
falls.
What is the man’s upward speed when his head is level with the bottom of the barrel? (Use
g = 10 m s–2.)
Question 3
A box of mass 8.0 kg rests on a horizontal, rough surface. A string attached to the box passes
over a smooth pulley and supports a 2.0 kg mass at its other end
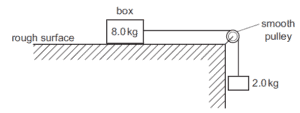
When the box is released, a frictional force of 6.0 N acts on it.
What is the acceleration of the box?
Question 4
The momentum of an object changes from 160 kg m s–1 to 240 kg m s–1 in 2 s.
What is the mean resultant force on the object during the change?
Question 5
Two spheres approach each other along the same straight line. Their speeds are u1 and u2
before collision. After the collision, the spheres separate with speeds v1 and v2 in the directions
shown below.
Which equation must be correct if the collision is perfectly elastic?
A u1 – u2 = v2 + v1
B u1 – u2 = v2 – v1
C u1 + u2 = v2 + v1
D u1 + u2 = v2 – v1
Solutions
Solution Q1
weight of the box is 20N
weight = mg
20 = m * 10
m = 2kg
since the box slide down the plane, it means there is a resultant force or net force
F – Fr = ma
F = force parallel to the plane = 10N
10 – 4 = 2 * a
6 = 2a
a = 3 ms-2
Solution Q2
The force acting in this questions are the weight of the man, the weight of the barrel and the tension on the rope.
As the man moves upward, this is what happens. The tension on the rope acting upward is greater than the weight of the man acting downward. So this gives a resultant force
mathematically,
T – wm = m1a1……..iing eqn i
wm represents the weight of the man
m1 is the mass of the man
a1 is the acceleration of the man
As the barrel moves downward. The tension on the rope acting upward is less than the weight on the barrel acting downwards. So this gives a resultant force
dont forget that weight(gravitational force) is always acting downwards to the centre of the earth.
mathematically,
wb – T = m2a2……..ii
wb = weight of the barrel
m2 = mass of the barrel
a2 = acceleration of the barrel
combining eqn i and ii and eliminate T
you will have
wb – wm =m2a2 + m1a1
note the two objects will have the same acceleration
a2 = a1
wb – wm = (m1 + m2) a1
wb = 120*10 = 1200N
wm = 80 *10 = 800N
1200 – 800 = (120 + 80) a1
400 = 200*a1
a1 = 2 ms-2
recall,
v2=u2+2as
the man and the barrel would have covered half of the distance when his head is level with the bottom of the barrel
i.e s = 9m
v2 = 0 + 2 * 2 * 9
v2= 36
v = 6 ms-1
Solution Q3
The same approach we use in Q2 is applicable here
wb – fr = (m1 + m2)a1
wb = is the weight of the box
m1 is the mass of the box, m2 is the mass at the other end
20 – 6 = 10 * a
14 = 10a
a = 1.4 ms-2
Solution to Q4
change in momentum = p1 – p2
change in momentum = 240 – 160 = 80kgms-1
resultant force = change in momentum / time = 80 / 2 = 40N
Recommended: Short note on dynamics
Solution to Q5
Before collision, the balls move in opposite direction to each other
After collision, the balls move in the same direction
recall that,
relative speed of approach = relative speed of separation
u1 – u2 = v2 – v1 ( when they are moving in the same direction both before and after collision)
But in this case, they move in opposite direction before collision
in this case
u1 + u2 = v2 – v1
The answer is D
OR
If you look closely, u1 and v1 are in the same direction, that means
u1 + v1
u2 and v2 are in opposite direction, that means
v2 – u2
using conservation of linear momentum
u1 + v1 = v2 – u2
rearrange
u1 + u2 = v2 – v1
D is the correct answer
More worked examples on CIE Physics Dynamics
Example 1
A ball of mass m. It is dropped onto a horizontal plate as shown in the figure below
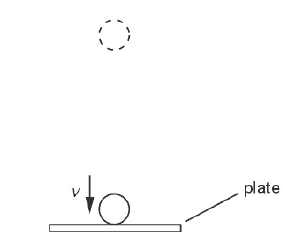
Just has the ball makes contact with the plate, it has a velocity v, momentum p and kinetic energy Ek.
- Write down the momentum p in terms of mass m and velocity v
- Show that Ek =p2/2m
iii. Just before the impact with the plate, the ball of mas 35g has speed 4.5ms-1. It bounces from the plate so that its speed immediately after losing contact with the plate is 3.5ms-1. The ball is in contact with the plate for 0.14s. Calculate for the time that the ball is in contact with the plate, the average force, in the addition to the weight of the ball, that the plate exert on the ball.
Solution
i p = mv
ii Ek = mv2/2 ……….. 1
p = mv ……………… 2
eqn1 can be written as
E_k=(m^2 v^2)/2m
therefore
Ek =p2/2m
iii.
Change in momentum ∆p= m(u+v)
The reason for positive sign is because the ball moves in opposite direction after rebound i.e ∆p = 0.035(3.5+4.5)
∆p=0.28〖kgms〗^(-1)
F= ∆p/∆t
F is the force of impact
F=0.28/0.14
F = 2N
Example 2
A ball falls vertically onto horizontal ground and rebounds, as shown
The ball has momentum p1 downwards just before hitting the ground. After rebounding, the ball
leaves the ground with momentum p2 upwards. The ball is in contact with the ground for 0.020 s.
During this time interval, an average resultant force of 25 N acts on the ball.
What is a possible combination of values for p1 and p2?
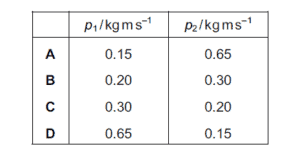
Solution
F= (p2- p1)/∆t
Since the ball is in opposite direction, it implies that
F= (p2+p1)/∆t
p2+p1 = 25* 0.02 = 0.5
Since the ball has the same mass the velocity before hitting the plate will be higher than the velocity after it bounces.
So therefore p1 > p2, from the option C is the correct answer.
