How to solve questions on Nuclear Physics for Cambridge A level

How to solve questions on Nuclear Physics for Cambridge A level

Question 1

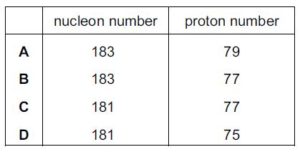
The gold nucleus 185Au79 undergoes alpha decay. What are the nucleon number and proton number of the nucleus formed by this decay?{cambridge A level may/june 2016 p12}

Solution

Au undergoes alpha decay

185Au79 – 181X77 + 4He2

The above equation is conserved since the number of nucleon and proton are the same before and after decay

The nucleon numberof the nucleus formed is 181 and the proton number is 77

C is the correct option

Question 2

In a time of 42.0 minutes, the count rate from the sample of copper-66 is found to decrease from 3.62 × 104 Bq to 1.21 × 102 Bq. Calculate the half-life of copper-66.{cambridge A level may/june 2016 p41}

Solution

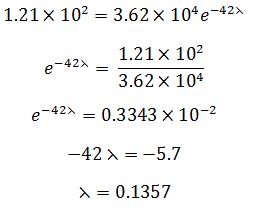
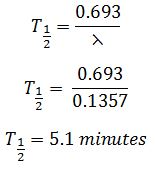
Question 3

The diagram shows part of a radioactive decay chain in which the nuclide thorium-232 decays by α-emission into radium-228. This nuclide is also unstable and decays by β-emission into a nuclide of actinium. This process continues.{cambridge A leve oct/nov 2015 p11}

What are X, Y and Z?

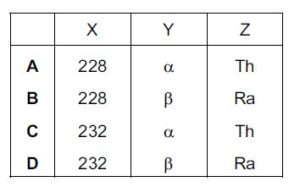
Solution

since Ra undergoes beta decay X will still be 228: beta decay does not affect nucleon number

Y is beta since Th nucleon number isnt affect and the proton increase by 1

Z is Ra since the proton number is 88, after Th has undergone alpha decay, having the same proton number with Ra making it an isotope of Ra

B is the correct option

Question 4

In a model of a copper atom of the isotope 63Cu29, the atom and its nucleus are assumed to be spherical. The diameter of the nucleus is 2.8 × 10–14 m. The diameter of the atom is 2.3 × 10–10 m.{cambridge A leve oct/nov 2015 p22}
Calculate the ratio

Solution

denisty of nucleus = mass of nucleus / volume of nucleus

volume of nucleus =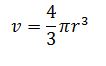

Volume = 4/3*3.142*(2.8×10^-14)^3

mass of nucleus = 63u

density of atom = mass of atom / volume of atom

volume = 4/3*3.142*(2.3×10^-10)^3

mass of atom = 63u

mass of atom and mass of nucleus (approx.) equal

ratio

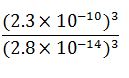
ratio = 5.5 x 10 ^11

Question 5

In the D-T reaction, a deuterium (2H1) nucleus fuses with a tritium (3H1) nucleus to form ahelium-4 (4He2) nucleus. The nuclear equation for the reaction iscambridge A level 2014 p41}

Some data for this reaction are given in Figure below

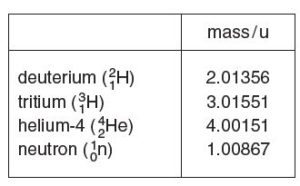
Use data from Figure above to determine the energy released in this D-T reaction.

Solution

total mass of the reactant = 2.01356 + 3.01551 = 5.02907 u

total mass of the product = 4.00151 + 1.00867 = 5.01018 u

mass defect = total mass of reactant – total mass of product = 5.02907 u – 5.01018 u

mass defect = 0.01889 u

note

1u is equivalent to 934 Mev

so,

0.01889 u = (933 * 0.01889) Mev

energy released in this D-T reaction = (934 * 0.01889) Mev = 17.6 Mev

Recommended: Question and answer on Nuclear for UTME

Recommended: Short notes on Nuclear physics