How to solve questions on stationary waves, diffraction and interference
How to solve questions on stationary waves, diffraction and interference
Question 1
A parallel beam of light of wavelength 450 nm is incident normally on a diffraction grating which has 300 lines / mm. What is the total number of intensity maxima observed?{ Cambridge A level may/jun 2016 p11)
A 7 B 8 C14 D15
Solution
![]()
d is the slit separation in meters
300 line is 1 mm
1 mm is 10^-3 m
1 line = 10^-3 / 300 m
d = 10^-3 / 300
wavelength = 450nm = 450 x 10^-9 m
the angle of diffraction = 90 in order to calculate the total number of maxima
n x 450 x 10^-9 = 10^-3 / 300 x sin 90
n = 7, which is the number of order
the total number of maxima = 2 x 7( 7 order up and 7 order down) + 1(zero order) = 15
D is the correct option
Question 2
Wave generators at points X and Y produce water waves of the same wavelength. At point Z, the waves from X have the same amplitude as the waves from Y. Distances XZ and YZ are as shown.
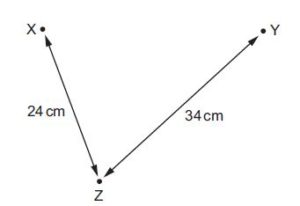
When the wave generators operate in phase, the amplitude of oscillation at Z is zero. What could be the wavelength of the waves?{ Cambridge A level May/jun 2015 p13}
A 2 cm B 3 cm C4cm D 6 cm
Solution
since the amplitude at z is zero, it means it is a destructive interference
yz – xz = (n + 1/2)ℷ
34 -24 = (n + 1/2)ℷ
10 = (n + 1/2)ℷ
n =1, 2, 3,4, ……..
using n = 2
10 = 2.5 ℷ
ℷ = 10/2.5
ℷ = 4 cm
Question 3
A parallel beam of white light passes through a diffraction grating. Orange light of wavelength 600 nm in the fourth order diffraction maximum coincides with blue light in the fifth order diffraction maximum. What is the wavelength of the blue light? {Cambridge A level may/jun 2014 p11}
A 450 nm B 480 nm C 500 nm D 750 nm
Solution
when one light coincides with another in diffraction grating
![]()
600 * 4 = 5 * ℷ
ℷ = 480 nm
B is the correct option
Question 4
The basic principle of note production in a horn is to set up a stationary wave in an air column.
For any note produced by the horn, a node is formed at the mouthpiece and an antinode is formed at the bell. The frequency of the lowest note is 75 Hz. What are the frequencies of the next two higher notes for this air column?
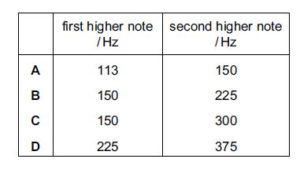
{Cambridge A level may/jun 2014 p11}
Solution
a node is formed at the mouthpiece and an antinode is formed at the bell means, one end is closed and the other end is opened.
for the lowest frequency(first harmonic)
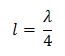
ℷ =4l
v = fℷ
v = 4lf
f = v / 4l
fo = 75 Hz
for second harmonic
L = 3ℷ / 4
ℷ = 4l / 3
v = fℷ
v = 4lf / 3
f = 3v / 4l
f = 3f0
f = 3 * 75 = 225 Hz
For 3rd harmonic
f = 5fo
f = 5* 75 = 375 Hz
D is the correct option
Question 5
Fig below shows a string stretched between two fixed points P and Q.
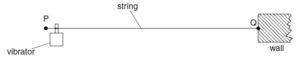
A vibrator is attached near end P of the string. End Q is fixed to a wall. The vibrator has a frequency of 50 Hz and causes a transverse wave to travel along the string at a speed of 40 m s–1.
Calculate the wavelength of the transverse wave on the string.{ Cambridge A level may/june 2013 p22)
Solution
v = f ℷ
40 = 50 * ℷ
ℷ = 40 / 50
ℷ = 0.8 m
Question 6
Light of wavelength 600 nm is incident on a pair of slits. Fringes with a spacing of 4.0 mm are formed on a screen. What will be the fringe spacing when the wavelength of the light is changed to 400 nm and the separation of the slits is doubled? { Cambridge A level may/ june 2013 p 11}
A 1.3 mm B 3.0 mm C 5.3 mm D 12 mm
Solution
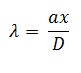
D is constant
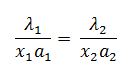
600 / 4*1 = 400 / 2x
x = 4 * 400 / 600 * 2
x = 1600 / 1200
x = 1.3 mm
Recommended: Note on stationary waves, diffraction grating and interference
