Notes On Deformation Of Solids For Cambridge A Level
Deformation can be referred to as change of shape. For this kind of deformation either a tensile force which is responsible for stretching or compressive force which is responsible for squashing must be applied for deformation to occur.
Hooke’s Law
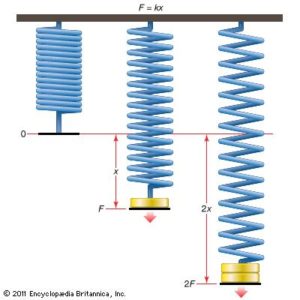
It states that provided the elastic limit is not exceeded, the extension(e) is directly proportional to the force applied
mathematically
F α e
F = Ke
F = force applied(N)
K = force constant (Nm-1)
e = extension(m)
It means before a material extends there must be force applied. This implies that extension depends on the force applied.
Extension: It is the change in length of a spring
Load: The weight attached to the spring
Graphicaly
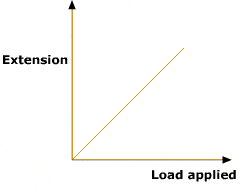
From this graph
force constant(k) = inverse of the graph’s slope
Another Hooke’s law graph
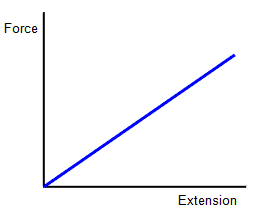
Force constant = the slope of the graph
The two graphs represent Hooke’s law. The only difference is how to calculate the force constant from the graphs.
Elastic limit:It is the maximum point where an elastic material can still return to its original size, shape, lenght and position if the force or load of distortion is removed.
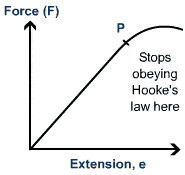
p is the elastic limit
Elastic deformation can be define as the change in shape/size/length/dimension when force is removed and its returns to original shape/size
Plastic deformation it is point beyond the elastic limit where an elastic material losses its elastic properties.
Strain energy: when an object has its shape changed by forces acting on it, the object is said to be strained. strain energy is energy stored in a body due to change of shape.
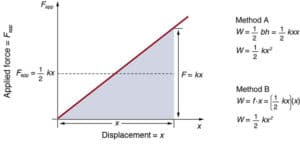
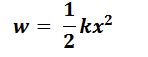
x = extension
Arrangement of spring in series and parallel
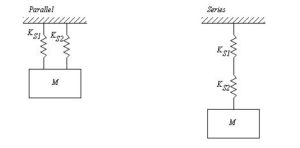
For the second springs arranged in series
The total extension =
![]()
Total force constant =
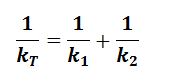
For the first springs arranged in parallel
Total extension =
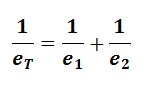
Total force constant =
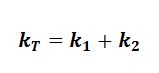
Young’s Modulus
It represents how easy it is to deform (stretch a material) or the measure of the stiffness of a material.
It can be define as the ratio of Tensile stress to tensile strain provided the limit of proportionality is not exceeded.
The Young’s modulus does not depend on the length of the wire but on the material that made the wirei.e increase on decrease in length of the wire doesn’t affect the youn modulus

Stress is the force per unit cross-sectional area of the wire
strain is the fractional increase in the original length of the wire
Measurement of the Young Modulus
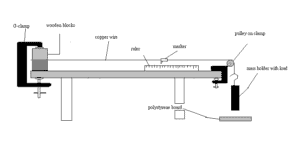
The Young’s modulus of this wire can be measured using this set up. The extension varies as the slotted masses changes. The extension can be detected as the marker on the wire changes position, and the new position being measured on the rule
What to measured and the measurement instrument
- initial length: A meter rule to measure the initial length
- diameter : A micrometer screw guage to measure the diameter of the wire
- extension: A marker and ruler to measure the extension
- force : A spring balance
Graphical representation of Young’s modulus
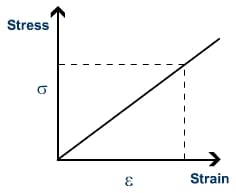
To calculate Young’s modulus, you will find the slope of the graph i.e the slope of the graph = Young’s modulus
Types of material
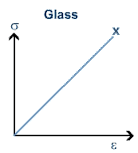
- Brittle : Materials break at the elastic limit. Example glass
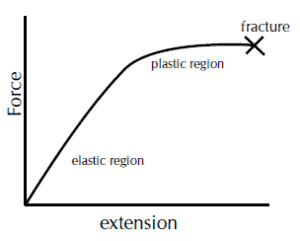
- Ductile : Materials become permanently deformed if they stretched beyond the elastic limit i.e they show plastic behaviour. Example Copper
Graph for brittle
Graph for ductile
Recommended: Solved questions on deformation of solids and kinematics
