Solutions to CIE Physics May/June And Oct/Nov P1 Questions
Below are few of the soluions to CIE physics 2015, 2016 and 2018 may/june Paper 1 questions.
Question 1
What is a unit for stress?
Solution
Stress = Force/Area = (Mass x acceleration)/(length x length) = Kgms^-2/m^2 = kgm^-1s^-2
Question 2
Physical quantities can be classed as vectors or as scalars. Which pair of quantities consists of two vectors?
A kinetic energy and force
B momentum and time
C velocity and electric field strength
D weight and temperature
Velocity and Electric field strength are both vector quantities. C is the correct answer
Question 3
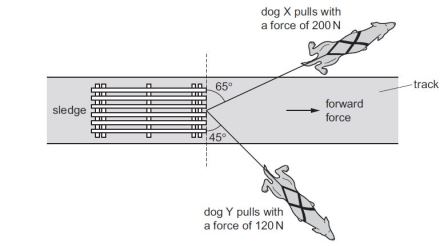
Two dogs pull a sledge along an icy track, as shown.

Dog X pulls with a force of 200 N at an angle of 65° to the front edge of the sledge. Dog Y pulls with a force of 120 N at an angle of 45° to the front edge of the sledge. What is the resultant forward force on the sledge exerted by the two dogs?
A 80 N B 170 N C 270 N D 320 N
Dog X with force 200N at an angle of 65
Let resolve into vertical and horizontal component (resolution of forces)
Horizontal component = 200 sin 65 = 181.2615
Vertical component = 200 cos 65 = 84.5236
Dog Y with force 120N at an angle of 45 to the front of the sledge
Vertical component = 120 cos 45 = 84.8528
Horizontal component = 120 sin 45 = 84.8528
Sum of the vertical forces = Vx – Vy ( Vx is in opposite direction to Vy, the reason for the negative sign) = 84.5236 – 84.8528 = -0.3292 N
Sum of the horizontal forces = Hx + Hy (same direction) = 181.2615 + 84.8528 = 266.1143 N
C is the correct answer
Question 4
The graph shown is that of resistance R of the thermistor (not current) against temperature T.
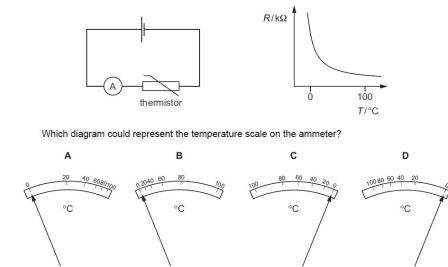
Solution
Ohm’s law: V = IR
Current I = V / R. So, the current is inversely proportional to the resistance R. The ammeter measures the current, not the resistance in a circuit.
The resistance falls rapidly with temperature at low temperatures, so the current will rise rapidly at low temperatures. Therefore, we need a larger region of the scale to represent a fixed amount of change in current at low temperatures. If the values on the scales are close to each other, the change in readings may not be noticeable.
The resistance curve becomes flatter at higher temperatures, so the current will change more slowly with temperature. Therefore, to represent this region of large temperature, a relatively smaller region of the scale is required. So, the values of the scale can be closer to each other.
A is the correct answer
Question 7
The graph shows the variation with mass of the weight of objects on a particular planet.
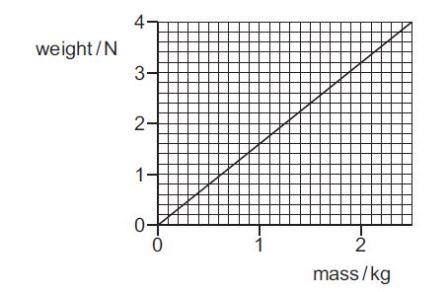
What is the value of the acceleration of free fall on the planet?
Solution
acceleration = gradient of the graph = dw/dm (taking the gradient at any point will give the same answer)
(3.2 – 0) /(2 – 0) = 3.2/2 = 1.6 ms-2
B is the correct answer
A 0.63 m s–2 B 1.6 m s–2 C 3.2 m s–2 D 9.8 m s–2
Question 10
A horizontal metal bar PQ of length 50.0 cm is hinged at end P. The diagram shows the metal bar viewed from above.
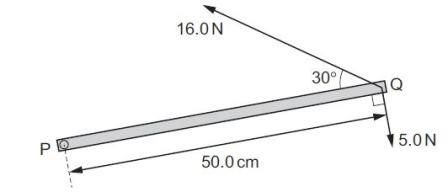
Two forces of 16.0 N and 5.0 N are in the horizontal plane and act on end Q as shown in the diagram.
What is the total moment about P due to the two forces?
Solution
Since forc 16N is acting at an angle which 30 then there is a need to do resolve the force. In this case to the vertical component.
Fv = 16 sin 30 = 8N (acting upward)
Note 5N is acting downward
The total force = 8N – 5N = 3N. The reason for the subtraction is because they acted in opposite direction
total moment about P = 3 x 50/100 = 1.5Nm
A 1.5 N m B 4.4 N m C 6.5 N m D 9.4 N m
Question 13
Liquids X and Y are stored in large open tanks. Liquid X has a density of 800 kg m–3 and liquid Y has a density of 1200 kg m–3.
At which depths are the pressures equal?
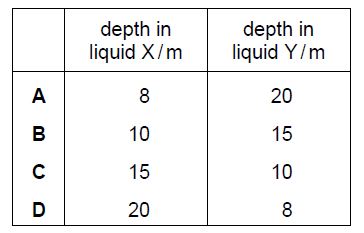
Solution
If pressurea are equal, then
Px = Py
hdgx =hdgy
acceleration of free fall is the same for the two liquid
800*hx = 1200*hy
2hx = 3hy
hx =1.5hy
this means that if hy = 10, then hx = 15
C is the right answer
Question 29
A charged particle is in the electric field between two horizontal metal plates connected to a battery, as shown. There is a force F on the particle due to the electric field.
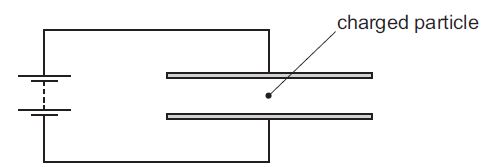
The separation of the plates is doubled.
What is the new force on the particle?
A F/4 B F/2 C F D 2F
Solution
Electric field between two parallel plates is an example of uniform electric field, meaning electric field strength is the same at any point in the field.
E = v/d = f/q
f = vq/d, q = fd/v
f1d1/v = f2d2/v
since the potential difference is the same
f1d1 = f2d2
d2 = 2* d1
f2 = f1/2, this means the force will be halved
B is the right answer
Question 39
How many down quarks are in a nucleus of hydrogen-3, 3H1 ?
A 2 B 3 C 4 D 5
Solution
The the nuclues of hydrogen-3, there are 1 proton and 2 neutron
Proton has (UUD) i.e. two up quarks and one down quarks
Neutron has (UDD) i.e. one up quarks and two down quarks
therefore, nucleus of hydrogen -3 = 1*(UUD) + 2*(UDD) = UUUUDDDDD
So there are five down quarks
D is the answer
If you need answers to any CIE Physics A level past questions especially P1, leave a comment.
Solutions to Cambridge A level (CIE) Physics Oct/Nov 2016 P1
The solutions below are guidlines to some topics I felt students want to see their solutions in cambridge A level Oct/Nov 2016 P11. You can comment below to ask any question you may find difficult in Oct/Nov 2016 P11, 12, and 13.
Question 1
The force F between two point charges q1 and q2, a distance r apart, is given by the equation
where k is a constant.
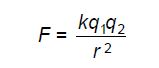
What are the SI base units of k ? {Cambridge A level oct/nov 2016, ques 2, p11}
Solution
The SI base unit of force is Kgms-2
Charge q1 is As
Charge q2 is As
distance r is m
SI base unit of k = (Kgms-2 x m) / (As x As) = Kgm2s-4A-2 (B is the correct option)
Question 2
A student uses a cathode-ray oscilloscope (c.r.o.) to measure the period of a signal. She sets the time-base of the c.r.o. to 5 ms cm–1 and observes the trace illustrated below. The trace has a length of 10.0 cm.
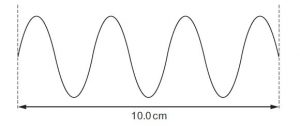
What is the period of the signal? {Cambridge A level oct/nov 2016, ques 5, p11}
Solution
From the graph there are 3.5 oscillations
The distance to cover one oscillations = 10/3.5 cm
Since the time-base of the c.r.o is 5 ms cm–1
The period of the signal = (10/3.5) x 5 = 14.3 ms = 1.4 x 10-2 s (D is the correct option)
Question 3
A cyclist pedals along a raised horizontal track. At the end of the track, he travels horizontally into the air and onto a track that is vertically 2.0 m lower.
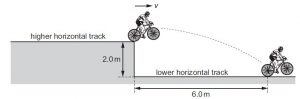
The cyclist travels a horizontal distance of 6.0 m in the air. Air resistance is negligible.
What is the horizontal velocity v of the cyclist at the end of the higher track? {Cambridge A level oct/nov 2016, ques 6, p11}
Solution
There are important points to note in this question:
The horizontal velocity v is used to calculate the horizontal distance
The time to reach the maximum height is the time to travel the horizontal distance
At maximum height u = 0
Using H = ut + 1/2gt2
2 = 0 + 1/2×9.81xt2
(t=0.6395s)
Horizontal distance = horizontal velocity(v) x time(t)
6 = 0.6395v
V = 9.4ms-2 (B is the correct option)
Question 4
A car is travelling at constant velocity. At time t = 0, the driver of the car sees an obstacle in the
road and then brakes to a halt. The graph shows the variation with t of the velocity of the car.
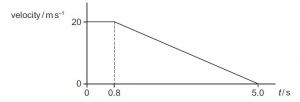
How far does the car travel in the 5.0 s after the driver sees the obstacle? {Cambridge A level oct/nov 2016, ques 8, p11}
Solution
The distance travelled by the car = 20 x 0.8 + ½ x 20 x(5 – 0.8) =16 +42 = 58m (C is the correct option)
Question 5
A car has mass m. A person needs to push the car with force F in order to give the car acceleration a. The person needs to push the car with force 2F in order to give the car acceleration 3a.
Which expression gives the constant resistive force opposing the motion of the car? {Cambridge A level oct/nov 2016, ques 11, p11}
Solution
Resultant force = applied force – resistive force
Ma = F- R
R = F- ma —-i
3ma = 2F – R
R = 2F – 3ma —–ii
Substitute for R in eq i
2F – 3ma = F – ma
F = 2ma
Therefore, R = 2ma – ma = ma
Resistive force = ma (A is the correct option)
Question 6
A car travels at a constant speed of 25 m s–1 up a slope. The wheels driven by the engine exert a forward force of 3000 N. There is a drag force due to air resistance and friction of 2100 N. The weight of the car has a component down the slope of 900 N.
What is the rate at which thermal energy is dissipated? {Cambridge A level oct/nov 2016, ques 20, p12}
Solution
Rate at which thermal energy is dissipated = power loss
Power = force x velocity
Rate at which thermal energy is dissipated = drag force x velocity = 25 x 2100 = 5.3 x 104 W (C is the correct option)
Question 7
Two parallel circular metal plates X and Y, each of diameter 18 cm, have a separation of 9.0 cm. A potential difference of 9.0 V is applied between them.
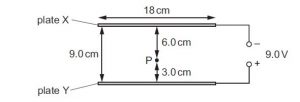
Point P is 6.0 cm from the surface of plate X and 3.0 cm from the surface of plate Y.
What is the electric field strength at P? {Cambridge A level oct/nov 2016, ques 30, p12}
Solution
The kind of field in this this is a uniform electric field. Therefore, at any point in the field the electric field strength is constant.
Electric field strength = potential difference / distance between the plate = 9 / 0.09
Electric field strength at P = 100 Nc-1 (B is the correct option)
You may like to download: Click here to download CIE A Level Physics Past papers 1 Solutions and E-book
Solutions to Cambridge A level (CIE) June 2015 and 2016 physics 9702
I took some questions out of 2015 and 2016 May/June Cambridge A level physics paper 11 and provid solutions to them based on their difficulty level. However, if you have any questions that you need additional explanation in 2015 and 2016 past papers, kindly comment below.
Question 1
The average kinetic energy E of a gas molecule is given by the equation E = 3/2 kT where T is the absolute (kelvin) temperature.
What are the SI base units of k ?
A kg–1m–1s2K B kg–1m–2s2K C kg m s–2K–1 D kg m2s–2K–1
Solution
The S.I base unit of Kinetic energy = Kgm2s-2
For temperature = K
K = E/T = kgm2s-2 / k
K = kgm2s-2k-1
D is the correct option
Question 2
A uranium-238 nucleus, 238U92 , undergoes nuclear decays to form uranium-234, 234U92 .Which series of decays could give this result?
A emission of four β-particles
B emission of four γ-rays
C emission of one α-particle and two β-particles
D emission of two α-particles and eight β-particles
Solution
alpha emission = 4He2
beta emission = 0e-1
For nucleon number and proton number to be conserved Uranium-238 must undergo one α-particle and two β-particles
C is the correct option
Question 3
A cell of e.m.f. 2.0 V and negligible internal resistance is connected to a network of resistors as shown.
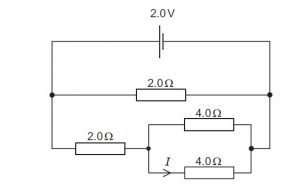
What is the current I ?
A 0.25 A B 0.33 A C 0.50 A D 1.5 A
Solutiothe two 4 ohms are in parallel
effective resistance is 1/R = 1/4 + 1/4
1/R = 2/4
R = 2 ohms
This 2 ohms is in series with the second 2 ohms
R = 2 + 2 = 4 ohms
This 4 ohms is in parallel with the 2 ohms above, therefore the same E.m.f flows through them
For the effective resistance of 4 ohms
E = IR
2 = I*4
I = 1/2 A
2 ohms and the two 4 ohms are in series, the same current will flow through them
The current that will flow through the 4 ohms = half of 1/2 = 1/4 = 0.25 A
A is the correct option
Question 4
A charged oil drop of mass m, with n excess electrons, is held stationary in the uniform electric field between two horizontal plates separated by a distance d.
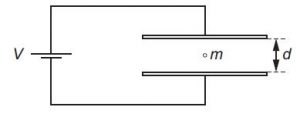
The voltage between the plates is V, the elementary charge is e and the acceleration of free fall is g.
What is the value of n ?
A eV/mgd B mgd/ev C meV/gd D gd/mev
Solution
Electric field intensity = F/ne = V/d
F = mg
mg/ne = V/d
mgd = neV
n = mgd /eV
B is the correct answer
Question 5
A sound wave has a speed of 330 m s–1 and a frequency of 50 Hz. What is a possible distance between two points on the wave that have a phase difference of 60°?
A 0.03 m B 1.1 m C 2.2 m D 6.6 m
Solution
V = fλ
330 = 50*λ
λ = 330/50 = 6.6 m
phase angle = 2πx/λ
π in rad = 180
60 = π/3
π/3 = 2πx/λ
λ = 6x
6x = 6.6
x = 1.1 m
B is the correct answer
Question 6
A fisherman lifts a fish of mass 250 g from rest through a vertical height of 1.8 m. The fish gains a speed of 1.1 m s–1.
What is the energy gained by the fish?
A 0.15 J B 4.3 J C 4.4 J D 4.6 J
Solution
P.E = mgh = 0.25*1.8*9.81 = 4.415 J
K.E = 1/2 mv2 = 1/2 * 0.25 *1.1^2 = 0.15 J
Energy gained by the fish = P.E +K.E = 4.4 + 0.15 = 4.6 J
D is the correct answer
Solutions to some questions in Cambridge A level May/June 2016 physics P11
Question 1
A car accelerates uniformly from velocity u to velocity v in time t.
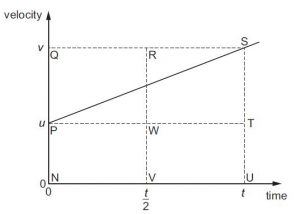
On the graph, which area equals the distance travelled by the car in time t ?
A NPTU + PQST B NPW V + VRSU C NPW V + WRST D PST + PQS
Solution
The distance covered by the car is NPSU which is a trapezium. The area under it will give the distance covered. In the trapezium there are three full boxes. The only option that gives three full boxes is option B.
Question 2
Two cars X and Y are positioned as shown at time t = 0. They are travelling in the same direction. X is 50 m behind Y and has a constant velocity of 30 m s–1. Y has a constant velocity of 20 m s–1.
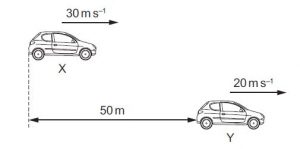
What is the value of t when X is level with Y?
A 1.0 s B 1.7 s C 2.5 s D 5.0 s
Solution
The time X will be at the same dstance with car Y is t
the distance covered for car X is
50 + s = 30t
the distance covered for car Y is
s = 20t
50 + 20t = 30t
50 = 10t
t = 5s
D is the correct option
Question 3
Two spheres approach each other along the same straight line. Their speeds are u1 and u2 before they collide. After the collision, the spheres separate with speeds v1 and v2 in the directions shown below.
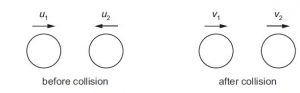
The collision is perfectly elastic. Which equation must be correct?
A u1 – u2 = v2 + v1
B u1 – u2 = v2 – v1
C u1 + u2 = v2 + v1
D u1 + u2 = v2 – v1
Solution
relative speed of approach = relative speed of separation for perfectly elastic collision
u1 + u2 = v2 – v1
D is the correct answer
Question 4
The diagram shows a man standing on a platform that is attached to a flexible pipe. Water is pumped through the pipe so that the man and platform remain at a constant height.
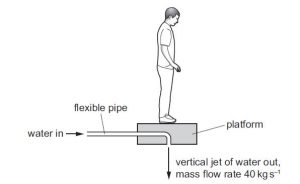
The resultant vertical force on the platform is zero. The combined mass of the man and platform is 96 kg. The mass of water that is discharged vertically downwards from the platform each second is 40 kg. What is the speed of the water leaving the platform?
A 2.4 m s–1 B 6.9 m s–1 C 24 m s–1 D 47 m s–1
Solution
The force exerted by the man and the platform = the vertical downward force of the water
96*9.81 = m * v/t
96 * 9.81 = m/t * v
v = 96*9.81 / 40 = 23.544 = 24ms-1
C is the correct option
Question 5
A solid metal cylinder stands on a horizontal surface, as shown.
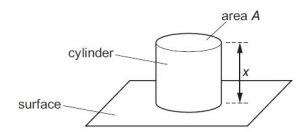
The cylinder has length x and cross-sectional area A. The cylinder exerts a pressure p on the surface. The acceleration of free fall is g. Which expression gives the density of the metal of the cylinder?
A gx/p B p/gx C gx/pA D pA/gx
Solution
pressure = force / area
area = A
P = F / A
F = PA
mass = force/acceleration of free fall
mass = PA / g
density = mass / volume
volume = A *x = Ax
density =( PA/g)/Ax = P /gx
B is the correct option
Question 6
A trailer of weight 30 kN is attached to a cab at X, as shown in the diagram.
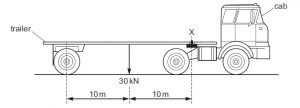
What is the upward force exerted at X by the cab on the trailer?
A 3 kN B 15 kN C 30 kN D 60 kN
Solution
F * 20 = 30 * 10
F = 300 / 20 = 15 KN
B is the correct answer
Question 7
Some gas in a cylinder is supplied with thermal energy q. The gas does useful work in expanding at constant pressure p from volume V0 to volume VF, as shown.
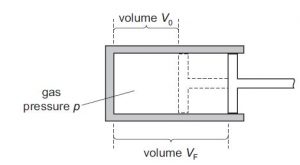
Which expression gives the efficiency of this change?
A pV0 / q B. Vf / Voq C. p(Vf – V0 ) / q D.(Vf – V0 )/V0q
Solution
Efficiency = workoutput / workinput
workinput = q
workoutput = p ( Vf – V0)
efficiency = p ( Vf – V0) /q
C is the correct option
Question 8
Two copper wires of equal length are connected in parallel. A potential difference is applied across the ends of this parallel arrangement. Wire S has a diameter of 3.0 mm. Wire T has a diameter of 1.5 mm.
What is the value of the ratio current in T/ current in S?
A. 1/4 B. 1/2 C. 2 D. 4
Solution
Resistance = (resistivity x length)/Area
Area = (pi x square of diameter)/4
length and resistivity is constant
meaning, Rs(ds)^2 = RT(dT)^2
RS/RT = (dS)^2/(dT)^2 = (3×3)/(1.5×1.5) = 4
Since the wires are connected in parallel, it means that the potential difference across each wire will be the same.
V = IR
IsRs = ItRt
It/Is = Rs / Rt = 4
i.e. the ratio current in T/ current in S = 4
D is the correct answer
