Notes on Kinematics – One Dimensional Motion and Projectile

Notes on Kinematics – One Dimensional Motion and Projectile

This note summarizes everything you need to know on kinematics in a simple way. It os brief and concise.

Definition of terms

Displacement: It is the distance moved in a particular direction. It is a vector quantity. The S.I unit is (m)

Velocity: It is the rate of change of displacement. It is a vector quantity. The S.I unit is (ms-1)

Speed : It is the rate of change of distance. It is a scalar quantity. The S.I unit is (ms-1)

Acceleration: It is the rate of change of velocity. It is a vector quanity. The S.I unit is (ms-2)

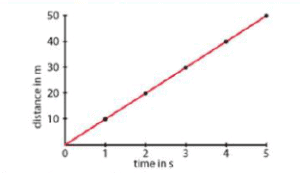
Uniform Speed: This is equal distance at equal time interval

Graphical representation of Uniform Speed

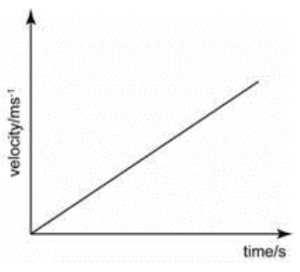
Uniform Acceleration: This is equal velocity at equal time interval

Graphical representation of uniform acceleration

Mathematical Expressions

speed = distance/ time = d / t

velocity = displacement / time  = d / t

Average speed : Total distance/ total time taken

Acceleration = change of velocity / time  = (v – u) / t

v  =  Final velocity

u  = initial velocity

Velocity – time Graph

The area under the graph of a velocity – time graph is  displacement

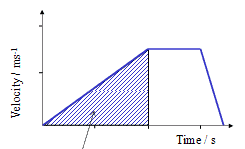
Since the diagram is a trapezium, we can calculate the total distance using the area of a trapezium

Let look at an example

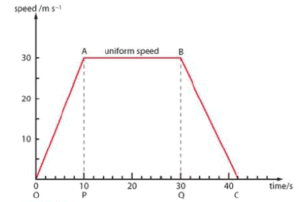
From the diagram above

i  what is the distance travelled during the first 10s

ii the total distance travelled

iii the average speed for the whole journey

Solution

i  using triange AOP = 1/2 * OP * AP = 1/2 * b * h = 1/2 * 10*30 = 150m

ii using Trapezium AOCBA = 1/2 *(AB + OC) * AP = 1/2 *(20 + 42) *30 = 1/2 * 62 *30 = 930m

ii average speed = total distance / total time taken

total time taken is 42s

average speed = 930 / 42 = 22.1 ms-1

Derive, from the definitions of velocity and acceleration, equations that represent uniformly accelerated motion in a straight line

v =u+at

s=[(u+v)/2]t

v²=u²+2as

s=ut+1/2at²

v = final velocity

u = initial velocity

t = time taken

s = distance covered

a = uniform acceleration

From the definition of acceleration

a = (v-u) / t

Cross multiply and rearrange

v = u + at

From average velocity,

Average velocity = s / t

Average velocity = (v +u)/2

equate the two equations together, you get

s / t = (v +u)/2

Cross multiply and rearrange

s = [(v + u)t]/2

Taking v = u + at ………i , and s = [(v + u)t]/2….ii

Substiturte v = u + at in eqn i into eqn ii, so you get,

s = ut + 1/2at²

Taking v = u + at…….i and s = [(v – u)t]/2…. ii

Make t the subject of the eqn in eqn i

t = (v – u) / a …………iii

substitute eqn iii into eqn ii, you get

v²=u²+2as

Motion of bodies falling in a uniform gravitational field without air resistance – Kinematics

In a uniform gravitational field, the gravitational field strenght is constant. The gravitational field strenght is also refer to as acceleration due to gravity (g).

Without air resistance means the air resistance is negligible or the drag force

The displacement – time graph, velocity – time graph, acceleration – time graph of such a motion is shown below

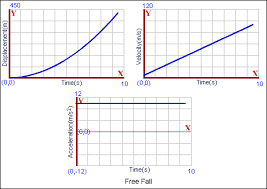
Always remember that the gradient or slope of displacement – time graph is velocity, the gradient of velocity-time graph is acceleration.

From the graph above, the acceleration-time graph shows that it is a uniform acceleration or a constant acceleration.

v =u+at

s=[(u+v)/2]t

v²=u²+2as

s=ut+1/2at²

in this case all you have to do is make a = 9.81ms-2, which the value of acceleration due to gravity. But in some cases you can be ask to make a = 10ms-2

The motion of bodies falling in a uniform gravitational field with air resistance

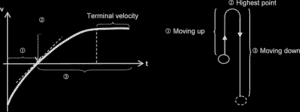
When any object moves through air, the air offers a frictional resistance (drag) to the motion. This causes the object to decelerate. The deceleration is not constant but depends on the velocity of the object. The faster the object the greater the resistance and deceleration. You can experience this when you run – the faster you run, the harder the air seems to blow against.

Graphical representaion of this kind on motion is shown below

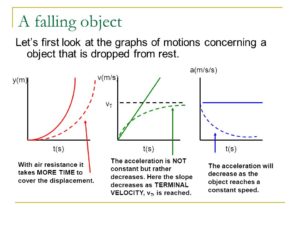
Where the arrow pointed shows the graph of displacement-time graph, velocity-time graph, acceleration-time graph when there is air resistance.

For displacement-time graph: it takes more time to cover because of the air resistance compared with when there is no air resistance

For velocity: the acceleration isnt constant because as the speed increases the air resistance increases until a time is reached when the the weight of the object equals the drag force(air resistance), at this point no resultant force acting on the body and it will fall with a constant speed, called the terminal velocity(this has being explained when i discussed dynamics)

Terminal velocity is the point at which the resultant force is zero.

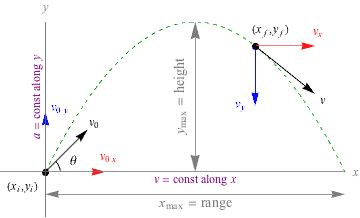
Motion due to a uniform velocity in one direction and a uniform acceleration in a perpendicular direction.

The type of motion to discuss here is a Projectile. Projectile is any object that is given an initial velocity and then follows a path determined entirely by gravitational acceleration.

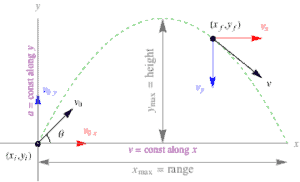
The initial velocity is at an angle of  θ. This initial velocity will be resolve into both vertical component and horizontal component.

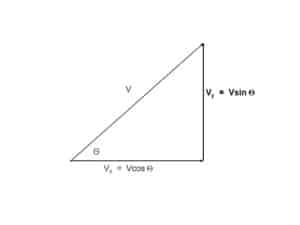
Using your SOHCAHTOA

the vertical component of the velocity will be usinθ

the horizontal component of the velocity will be ucosθ

horizontal component of the velocity has no force acting so it is constant

vertical component of the velocity has a constant force acting so there is a constant acceleration.

derivations

To calculate the time to reach the maximum height

v = u – at

at maximum height v = 0

0 = usinθ – at

t = usinθ / a

your a = 9.81ms-2

Time of flight = 2*t = 2usinθ / a

To calculate maximum height

v²=u² – 2as

at maximum height v = 0

u = usinθ

a = 9.81ms-2

s = maximum height

if you subsitute you get your maximum height

Horizontal distance (range)

v = d / t

the reason for this formula is because there is no force acting on it, which implies a uniform velocity

d= horizontal distance

v = horizontal component of velocity = ucosθ

t = time to complete the parabolic path ( which can be sometimes time of flight or time to reach the maximum height depending on the projectile diagram given). if it is a full diagram you use time of flight. if it is half of the full diagram you use time to reach the maximum height). The diagram above is a full diagram.

ucosθ = d / t

Recommended: Solved questions on motion