Simple Harmonic Motion Definition, Formulas, And Graphs
In this article, I will discuss the definition of simple harmonic motions, formulas, and graphs. Oscillation is one complete movement from the starting or rest position, up, then down and finally back up to the rest position. Examples are pendulum, the beating of the heart, vibration of a guitar string, the motion of a child on a swing e.t.c.
A free oscillation means:
- No energy loss
- No external force acting
- Constant energy
- Constant amplitude
Definition Of Simple Harmonic Motion
It is defined as the motion of a particle about a fixed point such that its acceleration a is proportional to its displacement x from the fixed point, and is directed towards the point.
Mathematically,
![]()
The negative sign tells us that the acceleration is always in opposite direction to the displacement x
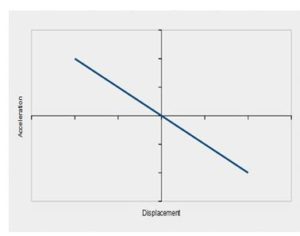
The slope or gradient of this graph = ω^2
Conditions necessary for a body to execute S.H.M
- when the body is displaced from equilibrium, there must exist a restoring force
- this restoring force must be proportional to the displacement of the body
(it is always directed to the equilibrium position)
a is acceleration
x is the displacement
Simple Harmonic Motion Formula
The major formula in SHM is ![]()
the w = 2 pi f where w is angular frequency (unit rad/s) and f is the frequency (unit Hertz)
Also, in S.H.M we can have v = wx, where v is the velocity and x is the displacement.
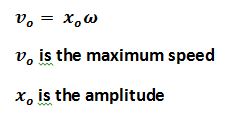
![]()
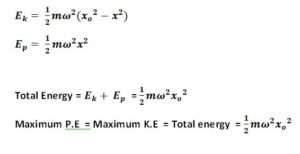
Understanding of terms
Period : it is the time taken for one complete oscillation
Frequency: it is the number of oscillations per unit time
Amplitude : it is the maximum displacement from the rest position.
Displacement : it is the distance from the equilibrium position
F= 1/T unit is Hertz (Hz)
F is frequency, T is period

Displacement And Velocity in Simple Harmonic Motion
Displacement and velocity in S.H.M varies with each other. The velocity is always maximum at the equilibrium position. Also, the displacement is maximum when the velocity is zero.
Simple Harmonic Motion Graphs
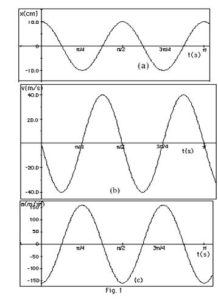
This means when displacement is maximum, velocity is zero and acceleration maximum but in opposite direction.
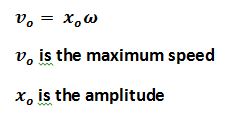
![]()
V is the instantaneous speed
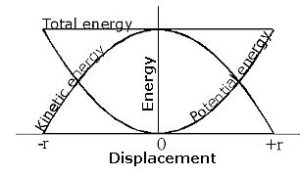
Interchange between Kinetic and potential energy
K. E is maximum when displacemet is zero
P.E is maximum when the displacement is maximum
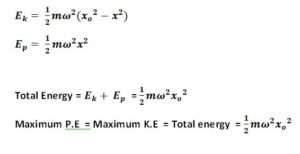
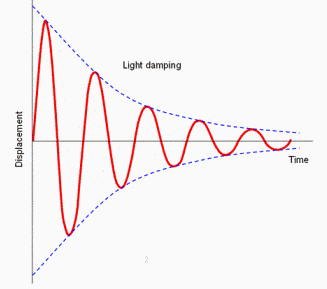
Damping
Damping is an influence within or upon an oscillatory system that has the effect of reducing oscillations
It can now be properly define as reduction in energy of oscillations/ reduction in amplitude due to force opposing motion/ resistive force.
Note
During damping amplitude of oscillation does not decrease linearly also the frequency of the oscillations does not change as the amplitude decreases.
Types of Damping
Light damping: Amplitude decreases gradually as the oscillations continues for a long time
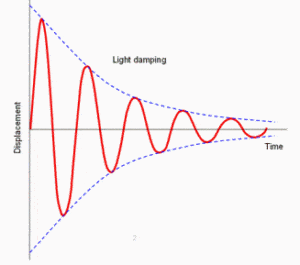
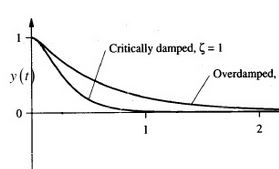
Critical damping: displacement decreases to zero in the shortest time without oscillation
Over damping : displacement decreases to zero in a longer time than for critical damping without any oscillation
Forced oscillation
This occur when an external force is applied to the original frequency causing a change in the frequency of the oscillation
For resonance to occur, there must be a system capable of oscillating freely and also have a way in which the system is forced to oscillate.
some terms
forced frequency: frequency at which object is made to vibrate
natural frequency of vibration: frequency at which object vibrates when free to do so
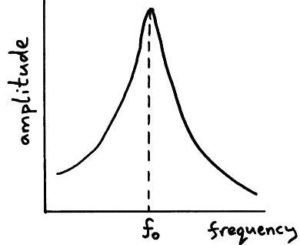
Resonance
resonance occurs when the natural frequency of vibration of an object is equal to the driving frequency giving a maximum amplitude of vibration
Uses of resonance
oscillation of a child’s swing
microwave to cook food
tuning of radio receiver
Problems of resonance
high-pitched sound waves can shatter fragile object
metal panels on machinery vibrate
