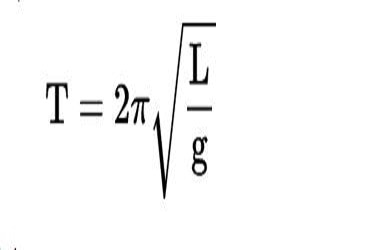
A simple pendulum consists of a bob attached to a string the other end of which is suspended from a firm support. If a simple pendulum is undisturbed, it is in equilibrium. To start it swinging, it must be pulled to one side of its equilibrium position. The forces on the mass are unbalanced and so it moves back towards its equilibrium position. The mass swings past this point and continues until it comes to rest momentarily at the other side; the process is then repeated in the opposite direction. Note that a complete oscillation is from right to left and back again. This is why a simple pendulum is an example of a simple harmonic motion.
Time Period Formula of a Simple Pendulum
Before I give the expression for the time period formula for a simple pendulum, there is need to list the assumptions made.
- In a simple pendulum, the string is inextensible
- The initial angle of oscillation is small
Note that period is defined as the time taken to complete one oscillation.
ω0 = 2πf
F = 1/T (f is frequency, T is the period)
ω0 = 2π/T
So , make T the subject of the equation
T = 2π/ω0 = 2π × √(L/g)
The period of a simple pendulum is affected by the following
- Length of the pendulum
- Acceleration due to gravity
Energy transformation
When the pendulum swings from end to end, the energy of the system changes from potential to kinetic and vice-versa, but at each stage of the swing, the total energy remains constant.
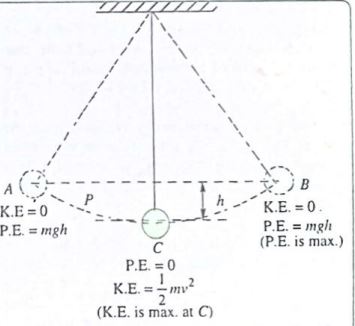
The pendulum swings from the highest point A through the centre of the swing C, to the other highest point B. At C, the bob is at the lowest position. Note this is a mechanical arrangement that demonstrate periodic motion. Therefore the potential energy of the system is zero. Also at C, the speed of the pendulum is maximum and so the kinetic energy is maximum at this point.
As the bob moves from C to B, the K.E at C is gradually transformed to P.E, with potential energy becoming maximum at B which is at a height h above C. At the point B, the total energy is potential energy and is equal to mgh. This is also P.E at A which is at the height above C as B.
We can find the maximum velocity of the swinging bob, which occurs as the bob passes through C. let this velocity be vmax. Since total energy is always conserved, we have
1/2mv2max = mgh
Hence v2max = 2gh
Vmax = square root of (2gh)
At A and B, the energy is all P.E. At C, energy is all K.E. At any intermediate point e.g P, the energy is partly potential and partly kinetic. At each point , however, the total energy (P.E + K.E) is constant and is equal to mgh.
