Discriminant and Nature of Roots In Quadratic Equation

A quadratic equation is an equation of the form ax² + bx + c = 0. The values of x that satisfy the quadratic equation are called the roots of the equation. The roots of a quadratic equation can be found by factorization, completing the square or using the formula. Before I can explain the discriminant, there is a need to fist express the quadratic formula. The formula makes it possible to express the roots of a general quadratic equation of the form ax² + bx + c = 0 in terms of the coefficients of a, b, and c. 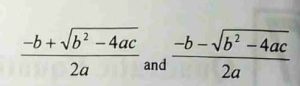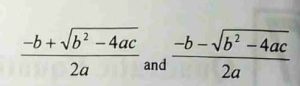Then the roots are now express as From the formula the discriminant is b² – 4ac. The value of b² – 4ac determine the nature of the roots of the equation:

• If b² – 4ac is positive or greater than zero, the two roots are real and different;
• If b² – 4ac is zero, the two roots are real and both equal to -b/2a
• If b² – 4ac is negative or less than zero, the quadratic equation has no real roots, i.e. the roots are complex numbers or imaginary.

From the conditions above, to have an equal roots, it means that b² – 4ac = 0. Read: Variation in mathematics and types

Determining the Quadratic equation from the roots

If α and β are the roots of the quadratic equation ax² + bx + c = 0, it can be shown that α + β = -b/a and αβ = c/a Once the roots α and β are known, the quadratic equation can then be written as X² + (b/a)x + c/a = 0 X² – (α + β)x + αβ = 0 Examples (1) If the equation y² + 3y + k = 0 has equal roots, the value of k is? As I have mentioned above, equal roots means b² – 4ac = 0, a = 1, b = 3 , and c = k 3² – 4(1*k) = 0 9 – 4k = 0 4k = 9 K = 9/4 (2) Find the quadratic equation whose roots are y = 7 and y = -2 α + β = 7 + (-2) = 7 – 2 = 5 αβ = 7 * (-2) = -14 Using y² – (α + β)y + αβ = 0 The equation will be y² – 5y -14 = 0